ℜ
Physik Chemie Grundschule Mathematik I Mathematik II Wissen
Kurze Worte Worte nach Alter Terme Rechner
Mathfeed Physfeed Philfeed
Das Lexikon Die Mission Die Autoren Copyright Impressum
Physik 5-10 Physik 11-13 Chemie 5-13 Mathe 5-8 Mathe 9-10 Mathe 10-13
☰
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 9 Ω
Das Banner der Rhetos-Website: zwei griechische Denker betrachten ein physikalisches Universum um sie herum.

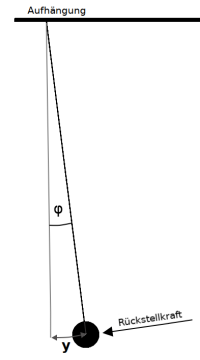
Fadenpendel

Physik

© 2016 - 2025


Basiswissen · Definition eines Fadenpendels · Fachworte zum Fadenpendel · Formeln für ein Fadenpendel · Legende · Das Fadenpendel als "einfache schwere Physik" · Fadenpendel und konservative Felder · Fadenpendel und generalisierte Koordinaten · Fadenpendel und Differentialgleichungen · Fußnoten


Basiswissen


Als Fadenpendel bezeichnet man einen oben befestigten Faden, der frei nach unten herabhängen kann und an dessem unteren Ende ein Gewicht befestigt ist. Ein Fadenpendel ist ein besonderes Kugelpendel.[8]



Bildbeschreibung und Urheberrecht
Ein Fadenpendel schwingt um seine Ruhelage. Für kleine Amplituden (Schwingungsweiten) gilt: die Auslenkung y als Funktion der Zeit ergibt dabei eine Sinusfunktion. Die Rückstellkraft ist immer in etwa proportional zur momentanten Auslenkung.☛


Definition eines Fadenpendels


Allgemein gesprochen sind Pendel Systeme, die durch die Schwerkraft am Schwingen gehalten werden. Ein Fadenpendel besteht aus einem Faden und einen Gewicht ganz unten am Faden sowie einem Aufhängungspunkt[7] oben. Wesentlich ist, dass die Masse des Fadens gegenüber der Masse des Gewichts vernachlässigt werden kann[1]. Eine Schaukel ist eine Art Fadenpendel. Siehe allgemein auch Schwingung ↗

Fachworte zum Fadenpendel


  • Die Lage des ungestört ruhenden Pendels nennt man die Ruhelage ↗
  • Die beim Schwingen größte Entfernung von der Ruhelage ist die Amplitude ↗

Formeln für ein Fadenpendel


  • Das Pendelgesetz[2]: T = 2·π·√(l/g)
  • Zur Auslenkung: b = φ·l

Legende


  • b: Die Auslenkung als Kreisbogenlänge

Das Fadenpendel als "einfache schwere Physik"


Der englische Schriftsteller George Orwell (1903 bis 1950) sprach gerne von "good bad poetry"[3] oder "good bad books".[4] In diesem Sinne könnte man das Fadenpendel auch als ideales Beispiel für einfache schwere Physik betrachten. Das Fadenpendel ist in seinem Aufbau sehr einfach zu verstehen. Auf das Pendel wirkt idealerweise nur die Schwerkraft ein, diese wirkt immer nur senkrecht nach unten. Die Ausgangssituation zeigt keinerlei Komplikationen. Und dennoch führt die genaue Berechnung der Geschwindigkeiten, Kräfte, Beschleunigungen und Ortslagen zu bestimmten Zeiten sehr schnell zu mathematisch sehr schweren und physikalisch sehr tiefsinnigen Prinzipien.

Fadenpendel und konservative Felder


Man spricht von konservativen Kräften oder Feldern konservativer Kräfte. Die Gravitationskraft ist eine solche konservative Kraft. Man nennt eine Kraft konservativ, wenn die Summe der potentiellen Energie V und der kinetischen Energie T eines Körpers bei einer Bewegung unter dem ausschließlichen Einfluss dieser Kraft immer konstant bleibt. Genau das trifft auf ein Fadenpendel zu: geht es von oben nach unten, wandelt sich potentielle Energie in kinetische Energie um. Steigt es von seinem tiefsten Punkt der Bewegung wieder auf, so wandelt sich kinetische Energie um in potentielle Energie. Wer tiefer in die Mathematik von Bewegungen in konservativen Feldern einsteigen möchte, kann sich dazu beispielsweise mit dem Maupertuis-Prinzip beschäftigen.[5] Siehe auch konservatives Feld ↗

Fadenpendel und generalisierte Koordinaten


Das Fadenpendel dient gerne als Beispiel für eine sogenannte generalisierte Koordinate. Die Kernidee ist die Frage: was ist die kleinste Anzahl von Angaben, die nötig sind, um die Lage eines Objektes zu beschreiben? Möchte man zum Beispiel die momentane Lage des Mittelpunktes der Masse unten am Fadenpendel, dem Gewicht beschreiben, könnte man dies über ein xy-Koordinatensystem machen. Man lässt das Pendel an einer senkrechten aufgestellten Tafel schwingen. Ist auf der Tafel ein Koordinatensystem gezeichnet, kann man die Position über je einen x- und y-Werte angeben. Wenn man aber die Länge des Fadens kennt, dann sind x und y nicht mehr voneinander unabhängig. Das heißt, eine der Koordinaten ist überflüssig. Es genügt tatsächlich, wenn man den Winkel φ der momentanen Auslenkung kennt. Aus der Kenntnis von φ und der Länge l des Fadenpendels kann man dann jederzeit, bei Bedarf die Koordinaen x und y berechnen. Statt zwei Koordinaten x und y genügt als die Angabe von φ als eine generalisierte Koordinate ↗

Fadenpendel und Differentialgleichungen


Eng verwandt mit den Ideen des konservativen Feld und der generalisierten Koordinaten ist Mathematik der Differentialgleichungen für ein Fadenpendel. Man kann darüber die Eigenfrequenz ω[6] eines Fadenpendels der Länge l bestimmen.

  • F ist dabei auch die rücktreibende Kraft, womit mit: -mg·s/l = m·a
  • Dabei ist s die Auslenkung von der Ruhelage in horizontalerRichtung, a die Beschleunigung und l die Länge des Fadenpendels. Das kleine g ist die Erdfallbeschleunigung. Der Bruch s/l ist damit gleich dem Tangens des Auslenkungswinkels gemessen am Punkt der Aufhängung.
  • Damit: d²s/dt² = a
  • Einsetzen: -mg·s/l = m·d²s/dt²
  • Division durch m, dann umstellen:
  • d²s/dt² + g·s/l = 0
  • d²s/dt² = -g·s/l
  • In Worten: zweimal ableiten von s nach der Zeit t führt auf die ursprüngliche Funktion mit dem konstanten Faktor -g/l.
  • Das passt auf s=cos(φ)
  • Man benötigt aber die Zeit t:
  • Mit φ=ω·t
  • Einsetzen: s=cos(ω·t)
  • Erste und zweite Ableitung bilden:
  • ds/dt = -ω·sin(ω·t)
  • d²s/dt² = -ω²·cos(ω·t)
  • Zweite Ableitung einsetzen in d²s/dt² + g·s/l = 0 gibt:
  • ω²·s-g·s/l = 0
  • Ausklammern von s:
  • s(-ω²+g/l) = 0
  • Gleichung gilt, wenn s=0 oder -ω²+g/l=0
  • Zweite Bedingung gibt:
  • ω²=g/l oder
  • ω = √(g/l) ✔

Differentialgleichungen werden in der Schulmathematik meist nur an einfachen Beispielen kurz vorgeführt. Tiefer behandelt werden sie normalerweise erst in einem Studium. Wer später nur wenige immer gleich bleibende Rechenwege benötigt, muss sich damit nicht beschäftigen. Wer aber in der Lage sein möchte, auch neuartige Problem auf dann vergleichsweise einfache Weise zu bearbeiten, für den lohnt sich eine beschäftigung mit der höheren Mathematik. Siehe auch Differentialgleichung ↗

Fußnoten


  • [1] Ein Pendel das nur aus einem steif gedacht Faden ohne zusätzliche Masse gedacht wird, verhält sich anders als ein Fadenpendel. Ein solches Pendel, ohne Zusatzmasse, bezeichnet man als Balkenpendel ↗
  • [2] Mit dem Pendelgesetz kann man die Dauer T einer Schwingung berechnen, wenn man die Pendellänge l und die Erdbeschleunigung g kennt. Es liefert sehr gute Ergebnisse bis hin zu Auslenkungen von etwa 45° für Versuche mit einer einfachen Stoppuhr. Siehe auch Pendelgesetz ↗
  • [3] Good bad poetry bringt ein tiefes Gefühl passend zum Ausdruck und geht in die Kultur eines Landes ein, obwohl man leicht erkennt, was mit dem Gedicht falsch ist. So sah es George Orwell (1903 bis 1950). Im Original: "There is a great deal of good bad poetry in English, all of it, I should say, subsequent to 1790." Unter anderem nennt er Kiplings Gedicht "Charge of the Light Brigade" als Beispiel. Das kennzeichnende Mekmal guter schlechter Gedichte ist ihre überdauernde Beliebheit trotz ihrer offensichtlichen Mangelhaftigkeit: "All of these reek of sentimentality, and yet – not these particular poems, perhaps, but poems of this kind, are capable of giving true pleasure to people who can see clearly what is wrong with them. One could fill a fair-sized anthology with good bad poems, if it were not for the significant fact that good bad poetry is usually too well known to be worth reprinting." In: George Orwell: Rudyard Kipling. Erschienen im Horizon, September 1941.
  • [4] Ein Beispiel für gute schlechte Bücher im Sinne Orwell ist Onkel Toms Hütte. Über dieses Buch schreibt er: "It is an unintentionally ludicrous book, full of preposterous melodramatic incidents; it is also deeply moving and essentially true; it is hard to say which quality outweighs the other." Weitere Beispiele sind Conan Doyles Sherlock Holmes Geschichten oder die im England seiner Zeit poplären Raffles-Geschichten. Das kennzeichnende Merkmal guter schlechter Bücher ist nach Orwell: "It is an unintentionally ludicrous book, full of preposterous melodramatic incidents; it is also deeply moving and essentially true; it is hard to say which quality outweighs the other." Orwell erkennt an, dass der Begriff "good bad book" auf den katholischen Schriftsteller G. K. Chesterton zurückgeht. In: George Orwell: Good Bad Books. Erschienen im Tribune, 2. November 1945.
  • [5] Das Maupertuis-Prinzip nutzt die Konstanz von potentieller und kinetischer Energie als eine sogenannte Zwangsbedingung zur Berechnung möglicher Bewegungsbahnen von Körpern durch Felder konsverativer Kräfte. Siehe mehr unter Maupertuis-Prinzip ↗
  • [6] Die Eigenfrequenz hängt mit der Schwingungsdauer T zusammen über: ω = 2π/T Pendelgesetz ↗
  • [7] Der Punkt, an dem der Faden eines Fadenpendels oben befestigt ist, wird als "Aufhängspunkt" bezeichnet in: Spektrum Lexikon der Physik. 6 Bände. Greulich, Walter (Hrsg.) Spektrum Akademischer Verlag. Heidelberg, Berlin. 1998-2000. Dort der Artikel "Zwangsbedingung". Siehe auch Freiheitsgrad ↗
  • [8] Fadenpendel ist ein Sonderfall von einem sphärischen Pendel, das heißt einem Kugelpendel: "Ein schwerer Punkt, der durch einen Faden konstanter Länge mit einem festen Punkte verbunden, im übrigen aber keiner weiteren Bedingung unterworfen ist, kann sich auf einer Kugelfläche bewegen, deren Mittelpunkt der feste Punkt und deren Radius die konstante Fadenlänge ist. Auch er heißt in etwas erweitertem Sinne ein einfaches Pendel, und zwar ein sphärisches oder auch, weil der Faden während der Bewegung eine Kegelfläche beschreibt, ein konisches Pendel." In: Lueger, Otto: Lexikon der gesamten Technik und ihrer Hilfswissenschaften, Bd. 7 Stuttgart, Leipzig 1909., S. 61-63. Siehe auch Kugelpendel ↗