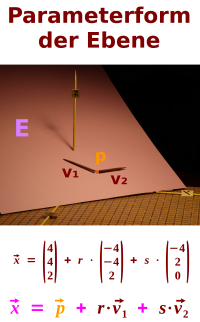
Parameterform der Ebene
Vektorrechnung
© 2016
- 2026
Basiswissen|
Schreibweise|
Legende|
Ebenenname|
Was heißt hier Ebene?|
Was besagt der Stützvektor?|
Die Spann- oder Richtungsvektoren v1 und v2|
Was bedeutet der Spannvektor v2 anschaulich?|
Was bedeutet der Spannvektor v2 anschaulich?|
Aus 3 Punkten aufstellen|
Umwandlungen, Parameterform ist gegeben|
Umwandlungen, Parameterform ist gesucht
Basiswissen
E: x = p + r mal v1 + s mal v2: p ist der Stützvektor und v1 und v2 sind die zwei Richtungsvektoren: wie diese Gleichung eine Ebene im Raum beschreibt, ist hier kurz erklärt.
Schreibweise
- E: x = p + r·v1 + s·v2
Legende
- E ist der Name der 👉 Ebene
- x ist ein beliebiger 👉 Ortsvektor
- p ist der sogenannte 👉 Stützvektor
- r ist ein sogenannter 👉 Laufparameter
- v1 ist der erste von zwei 👉 Spannvektor[en]
- s ist ein sogenannter 👉 Laufparameter
- v2 ist der zweite von zwei 👉 Spannvektor[en]
Ebenenname
- Man gibt den Namen einer Ebene meist mit einem Großbuchstaben an.
- Üblich ist das große E, oder auch D, F oder G.
- Man schreibt den Namen ganz links.
- Dahinter folgt ein Doppelpunkt.
Was heißt hier Ebene?
Eine Ebene - oft abgekürzt als E - in der Vektorrechnung ist eine flache, gerade Fläche in einem 3D-Raum. Sie ist unendlich ausgedehnt, hat also keine Ränder. Um sie eindeutig zu definieren, kann man (irgend)einen Punkt auf der Ebene angeben. Das ist der Stützpunkt. Dann gibt man zwei (fast) beliebige Vektoren an, zu denen die Ebene parallel sein soll. Das sind die zwei Richtungsvektoren. Mit diesen Angaben ist die Ebene eindeutig definiert. Siehe auch 👉 Ebene
Was besagt der Stützvektor?
Der Stützvektor ist ein spezieller Ortsvektor. Er beginnt im Koordinatenursprung und zeigt mit seiner Pfeilspitze - jeder Vektor ist ein Pfeil mit Spitze - auf den sogenannten Stützpunkt der Ebene. Der Stützpunkt ist ein Punkt, durch den die Ebene auf jeden Fall immer geht. Er stützt die Ebene sozusagen im unendlich ausgedehnten Raum irgendwo fest ab. Noch aber kann die Ebene um diesen Punkt gedreht werden. Also ist die Ebene noch nicht eindeutig festgelegt. Um der Ebene diese Freiheit zu nehmen, gibt man noch zwei Richtungsvektoren an. Siehe auch 👉 Stützvektor
Die Spann- oder Richtungsvektoren v1 und v2
Die beiden Vektoren v1 und v2 heißen Spann- oder auch Richtungsvektoren. Sie zusammen bestimmen, wie gekippt oder gedreht die Ebene im Raum liegt. Bei Ebenen kann man wahlweise von Spann- oder Richtungsvektoren sprechen. Bei ähnlich gedachten Geraden spricht man hingegen immer nur von Richtungsvetoren. Wie zwei ausgestreckte Arme eine Tischdecke aufspannen können, so spannen die Spannvektoren eine Ebene auf.
Was bedeutet der Spannvektor v2 anschaulich?
Man denkt sich den ersten Richtungsvektor, oft v1 genannt, mit seinem Anfang im Stützpunkt. Die Pfeilspitze zeigt dann vom Stützpunkt weg. Jetzt fordert man, dass die Ebene E sowohl den Stützpunkt als auch den Richtungsvektor v1 enthält. Damit hat man der Ebene einen Freiheitsgrad genommen: man kann sie jetzt nur noch in eine Richtung drehen. Siehe auch 👉 Richtungsvektor
Was bedeutet der Spannvektor v2 anschaulich?
Wie bei v1 denkt man sich auch den Richtungsvektor v2 mit seinem Anfang - also dem Ende ohne Pfeil - im Stützpunkt. Die Pfeilspitze zeigt dann vom Stützpunkt weg. Jetzt fordert man, dass die Ebene E sowohl den Stützpunkt als auch den Richtungsvektor v1 und auch v2 enthält. Damit hat man der Ebene endgültig alle Freiheitsgrade der Bewegung genommen: sie ist jetzt eindeutig festgelegt.
Aus 3 Punkten aufstellen
- Gegeben z. B.: P1, P2 und P3
- Einen beliebigen Punkt zum Stützvektor (Stützpunkt) machen.
- Dann aus P2-P1 den ersten Spannvektor v1 machen.
- Dann aus P3-P1 den zweiten Spannvektor v2 machen.
Umwandlungen, Parameterform ist gegeben
In der Vektorrechnung kann man Ebenen auf sehr viele verschiedene Arten darstellen. Wie man von der Parameterdarstellungen zu anderen Darstellungsformen kommt ist kurz erlärt in den folgenden Artikeln: