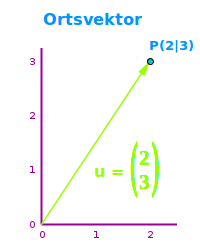
Ortsvektor
Ein Vektor der vom Koordinatenursprung aus gedacht wird
Basiswissen
Ein Vektor, dessen hinteres Ende im Ursprung eines Koordinatensystem gedacht wird zeigt mit seiner Spitze auf einen Punkt im Koordinatensystem. Jeder so gedachte Vektor heißt Ortsvektor.
Definition
- Der Punkt (0|0|0) heißt auch Koordinatenursprung.
- Ein Ortsvektor beginnt gedanklich immer im Koordinatenursprung.
- Seine Spitze zeigt dann auf irgendeinen Punkt im Koordinatensystem.
- Gedanklich führt der Vektor vom Ursprung zu dem Punkt an seiner Spitze.
- Die Vektorspitze zeigt also sozusagen auf den Ort eines Punktes.
- Daher kommt der Name.
Schreibweise eines Ortsvektors
- Bei einem 3D-Vektor schreibt man die Zahlen meist senkrecht übereinander.
- Die drei Zahlen heißen Vektorkoordinaten ↗
- Bei Punkten stehen die drei Zahlen nebeneinander.
- Bei Punkten heißen sie nur Koordinaten ↗
- Siehe auch Vektorschreibweisen ↗
Beispiel für einen Ortsvektor
- Der Ortsvektor mit den Komponenten 3, 4 und 10 zeigt mit seiner Spitze auf den Punkt (3|4|10). Siehe auch 3D-Punkt ↗
Ortsvektoren bei Geraden: der Stützvektor
Bei Gleichungen von Geraden und Ebenen kommt immer ein Ortsvektor, der sogenannte Stützvektor vor. Die Stützvektoren sind dann Vektoren, die vom Koordinatenursprung auf einen Punkt der Geraden oder Ebene gehen. Damit ist jeder Stützvektor immer auch ein Ortsvektor. Nun kommt ein Gegenbeispiel: man kann sich einen Ortsvektor vorstellen, der aber nichts mit Geraden oder Ebenen zu tun hat. Dann gibt es in diesem Zusammenhang auch keinen Stützpunkt. Dann macht es auch wenig Sinn, von einem Stützvektor zu reden. Der Ortsvektor ist dann einfach ein Ortsvektor aber kein Stützvektor. Lies mehr unter Stützvektor ↗
