ℜ
Physik Chemie Grundschule Mathematik I Mathematik II Wissen
Kurze Worte Worte nach Alter Terme Rechner
Mathfeed Physfeed Philfeed
Das Lexikon Die Mission Die Autoren Copyright Impressum
Physik 5-10 Physik 11-13 Chemie 5-13 Mathe 5-8 Mathe 9-10 Mathe 10-13
☰
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 9 Ω
Das Banner der Rhetos-Website: zwei griechische Denker betrachten ein physikalisches Universum um sie herum.

g-Kraft

Physik

© 2016 - 2025


Basiswissen · Die g-Kraft und die Änderung von Geschwindigkeit · Die g-Kraft und das Zweite Newtonsche Axiom · Die Einheit g als Vielfaches der Erdbeschleunigung · g-Kräfte beim Start von Raumfahrzeugen · g-Kräfte beim Wiedereintritt von Raumfahrzeugen · g-Kräfte in der Fliegerei · 0g bei einem Parabelflug · g-Kräfte bei Unfällen · Die Berechnung von g-Kräften · g-Kräfte bei einem leichten Hammerschlag · g-Kräfte beim Schaukeln · g-Kräfte bei einer Salatschleuder · Zusammenfassende Beispielwerte für g-Kräfte · Körperliche Effekte bei unterschiedlichen g-Kräften · Positive g-Werte · Negative g-Werte · Gegenmaßnahmen · Fußnoten


Basiswissen


Als g-Kraft bezeichnet man vor allem in der Fliegerei und der (bemannten) Raumfahrt Kräfte, die durch eine schnelle Änderung der Geschwindigkeit auftreten. Von 0g bei einem Parabelflug über 7g bei der Rückkehr von Mondflügen bis zu 180g bei schweren Unfällen: mit einigen Beispielen ist hier kurz die Physik der g-Kräfte vorgestellt.



Bildbeschreibung und Urheberrecht
Fliegt ein Flugzeug eine nach oben geöffnete Kurve, so wird man stärker in den Sitz gedrückt als bei einem waagrechten Geradeausflug. Das veranschaulicht gut die Grundidee der g-Kraft. © Unbekannt ☛



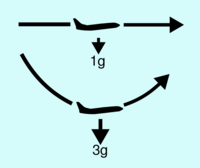
Dieses Bild ist für das Verständnis des Textes nicht wichtig. Das Bild wird im Text nicht erwähnt.
Hohe g-Kräfte treten oft dann auf, wenn enge Kurven mit hoher Geschwindigkeit gefahren oder geflogen werden. Das ist aber nur eine von mehreren Möglichkeiten.

Die g-Kraft und die Änderung von Geschwindigkeit


Solange auf einen Körper keine Kräfte von außen einwirken, ändert er seine Geschwindigkeit weder nach der Größe (wie schnell) noch nach der Richtung. Diese Gesetzmäßigkeit nennt man das erste Newtonsche Axiom. Und es gilt auch der Umkehrschluss: ändert ein Körper seinen Bewegungszustand nicht, so gibt es auch keine resultierenden Kräfte, die von außen auf ihn einwirken[2].

MERKSATZ:

1.0 Ohne Änderung der Geschwindigkeit keine äußeren Kräfte. Und: ohne äußere Kräfte keine Änderung der Geschwindigkeit.

Die g-Kraft gibt dann an, wie viel mal so stark eine Kraft von außen wirkt, wie bei einem unbewegten Aufenthalt auf der Erdoberfläche. Wenn ein Kampfpilot in einer engen Kurve zum Beispiel 9g erfährt[10], dann wirken von außen auf seinen Körper 9 mal so starke Kräfte, wie bei ruhigen Sitzen am Erdboden. Das ist die anschauliche Bedeutung einer Angabe von g-Kräften.

Die g-Kraft und das Zweite Newtonsche Axiom


F=ma ist die kurze Fassung des Zweiten Newtonschen Axioms: Kraft gleich Masse mal Beschleunigung. Man kann damit die Größe der Kraft berechnen, die ein Körper der Masse m spürt, wenn sich seine Geschwindigkeit mit der Beschleunigung a verändert[3]. Diese Kraft F in der Formel Newtons ist identisch mit der hier betrachteten g-Kraft.

MERKSATZ:

2.0 F=ma heißt: bei starken Beschleunigungen muss es starke äußere Kräfte geben.

Man stelle sich zum Beispiel einen Golfball auf dem sogenannten Tee vor, einem kleinen T-förmigen Holz. Nun schlägt der Spieler mit dem Schläger den Ball plötzlich aus seiner Ruhelage weg. In kurzer Zeit hat der Golfball eine hohe Geschwindigkeit erreicht[4]. Man kann dann umgekehrt folgern, dass auf ihn sehr hohe Kräfte von außen eingewirkt haben müssen. Wie groß diese Kräfte sind, berechnet man zum Beispiel über die Formel F=ma ↗

Die Einheit g als Vielfaches der Erdbeschleunigung


In der Fliegerei und der Raumfahrt bezeichnet man die Kräfte infolge von einer Änderung der Geschwindigkeit oft als g-Kraft. Das kleine g steht dabei für die Beschleunigung bei einem freien Fall. Das sind auf der Erde um die 9,81 m/s² oder rund 10 m/s². Wird man am Fallen gehindert, etwa wenn man auf dem Boden steht, so muss der Boden von außen mit einer Kraft auf den Körper einwirken. Das ist dann die Kraft von einem g. Beschleunigt man mit 20 m/s², so muss das Fahrzeug mit einer Kraft von 2g auf den Körper einwirken.

MERKSATZ:

3.0 Ein g entspricht der Kraft, die an einem Körper von außen angreifen muss, um ihn am freien Fall nahe der Erdoberfläche zu hindern.

Wirkt auf einen Körper doppelt so viel Kraft ein, wie ihn am Fallen auf der Erde hindern würde, so sind das 2g. Man schreibt das kleine g oft kursiv und und fügt es ohne Lücke direkt an die vorangehende Zahl an.

g-Kräfte beim Start von Raumfahrzeugen


Startet ein Rakete oder eine Raumfähre, so liegen die Astronauten meist mit dem Rücken nach unten. Die Anziehungskraft der Erde zieht sie nach unten. Aber der Sitz drückt mit einer Kraft dagegen und hält sie in ihrer Lage. Die wirkende Kraft entspricht 1g[16]. Nun startet die Rakete. Sie bewegt sich mit zunehmender Geschwindigkeit nach oben. Es ist letztendlich der Sitz des Astronauten, der diese Bewegung auf den Menschen übertägt: die Rakte drückt über den Sitz auf den menschlichen Körper und nimmt ihn so auf ihrer Bahn mit. Dabei werden bis etwa 4g erreicht.

MERKSATZ:

4.0 Etwa 3 bis 4g bei der Space Shuttle und bis zur 5g bei den Apollo-Mondflügen. Es sind die Sitze, die die Kräfte übertragen.

Wenn eine Raumfähre wie die US-amerikanische Space Shuttle dann etwa 8 Minuten nach dem Start mit fast 30 m/s² beschleunigt, dann wirken zunächst die 10 m/s² der Erdanziehung sowie zusätzlich noch die Kräfte zur Beschleunigung der Astronauten über die Sitze, also 30 m/s². Somit spüren die Raumfahrer beim Start eine Gesamtkraft entsprechend 4g[5]. Beim Aufstieg einer Saturn-V Rakete für das amerikanische Mondflugprogramm wurden nach etwa 150 Sekunden mit fast 5g die größten Beschleunigungskräfte erreicht[16]. Siehe auch Space Shuttle Aufstiegsdaten ↗

g-Kräfte beim Wiedereintritt von Raumfahrzeugen


Wenn Raumschiffe vom Weltraum kommend in die Erdatmosphäre eintreten, werden sie durch die Luftreibung stark abgebremst. Die Raumfähre Space Shuttle bremste dabei in rund 12 Minuten von 7800 m/s auf rund 3600 m/s ab. Dabei traten g-Kräfte von etwa 1,7g auf[6]. Beim amerikanischen Mondflugprogramm Apollo traten in der Raumkapsel beim Wiedereintritt in die Atmosphäre kurzzeitig bis über 7g auf[7].

MERKSATZ:

5.0 Beim Apollo-Programm (Mondflüge) wurden beim Wiedereintritt Werte von über 7g erreicht. Mit 1,7g sind die g-Kräfte bei modernen Raumfähren beim Wiedereintritt eher gering.

Das Beispiel des Wiedereintritts zeigt, dass g-Kräfte nicht nur auftreten, wenn etwas an Geschwindigkeit zunimmt. Auch beim Bremsen, oder oft gerade dann, treten hohe g-Kräfte auf. Im Kalten Krieg unternahm ein Amerikaner viele Versuche, bei denen er sich sich in kürzester Zeit mit einem Raktenschlitten abbremste. Dabei traten Werte von bis zu 45g auf[8].

g-Kräfte in der Fliegerei


Während in der Raumfahrt die hohen g-Kräfte meist durch eine Erhöhung oder Verringerung der Geschwindigkeit bei mehr oder minder geraden Flugbahnen auftreten, sind es in der Fliegerei vor allem Änderungen der Flugrichtung, die zu hohen g-Kräften führen. Wenn man mit großer Geschwindigkeit geradeaus fliegt und dann schnell in eine enge Kurve geht, treten hohe g-Kräfte auf.

MERKSATZ:

6.0 In der Fliegerei ist es oft eine schnelle Änderung der Flugrichtung, die zu hohen g-Kräften führt. Das betrifft vor allem Piloten von Kampfflugzeugen. Bis zu 9g sind üblich.

Treten bereits beim Katapultstart von Kampfflugzeugen g-Kräfte von 3 bis 3,5g auf[9], so müssen Piloten bei engen Kurven Werte von bis zu 9g aushalten[10]. Um die Physik der Kräfte zu verstehen, muss man auch hier daran denken, dass nach Newtons erstem Axiom ein Körper solange seinen eigenen Bewegungszustand beibehält, wie keine resultierenden Kräfte von außen auf ihn wirken. Bei einem engen Kurvenflug eines Flugzeuges ist es wie auch bei Raumflügen der Sitz des Piloten, der diese Kräfte überträgt.

0g bei einem Parabelflug


Ein interessanter Sonderfall ist ein sogenannter Parabelflug. Zu Forschungszwecken, aber auch für Touristen, kann bei einem solchen Flug für etwa 20 Sekunden am Stück Schwerelosigkeit simuliert werden. Die Flüge werden mit umgerüsteten Verkehrsmaschienen durchgeführt[17].

MERKSATZ:

7.0 Bei einem Parabelflug können auch Touristen 0g erfahren.

Die Grundidee ist es, dass ein Flugzeug nach einer Anlaufphase in einen steilen Steigflug übergeht und dann die Triebwerke ausschaltet. Ab dann sind sowohl die Passagiere wie auch das Flugzeug in einem freien Fall[18]. Je nach Flugbahn kann die Erfahrung zwischen 20 bis 30 Sekunden dauern. Siehe mehr dazu unter freier Fall ↗

g-Kräfte bei Unfällen


Die bisher betrachteten g-Kräfte traten zwar alle in extremen Situationen auf, waren aber mehr oder minder geplant und vorhersehbar. Anders sieht es bei Unfällen aus. Auch wenn der englische Rennfahrer Purley bei einem Unfall 180g überlebte[1], ist das doch eher die Ausnahme. Bei vielen Unfällen ist nicht alleine die Höhe der Anfangsgeschwindigkeit wichtig, sondern vor allem die Kürze der Strecke, über die diese auf 0 abgebaut wird.

MERKSATZ:

8.0 Bei Unfällen ist es oft die Kürze der Bremsstrecke, die lebensbedrohlich wird. Dass 180g am ganze Körper überlebt werden, ist die Ausnahme.

Das erklärt auch, warum man bereits beim Sturz mit dem Kopf auf einen harten Stein tödliche Verletzungen erleiden kann. Angenommen, man fällt aus einem Meter Höhe ungebremst mit dem Kopf voran nach unten. Dann prallt man mit einer Geschwindigkeit von etwa 0,45 m/s auf den Boden. Wenn der Beton sehr hart ist, wird diese Bewegung auf einer Strecke von vielleicht nur 1 Millimeter abgebremst (wenn Beton überhaupt so viel nachgibt). Dabei würden Bremskräfte von rund 100g auf den Kopf einwirken.

Die Berechnung von g-Kräften


Mit den Formeln v=at und s=½at² kann man selbst abschätzen, welche g-Kräfte bei Beschleunigungsvorgängen mindestens auftreten. Kennt man die Anfangsg√eschwindigkeit v und die Bremsdauer t, so kann man mit der ersten Formel[11] sofort die Beschleunigung ausrechnen. Diese geteilt durch 10 gibt in etwa den g-Wert. Kennt man nur die Anfangsgeschwindigkeit und die Bremsstrecke, so verbindet man die zwei Formeln zu a=v²/(2s).

  • Anfangsgeschwindigkeit und Beschleunigungszeit: a=v/t -> geteilt durch 10 gibt den g-Wert
  • Anfangsgeschwindigkeit und Beschleunigungsstrecke: a=v²/(2s) -> geteilt durch 10 gibt den g-Wert
  • Radius und Bahngeschwindigkeit bei einer Kreisbewegung: a=v²/r -> geteilt durch 10 gibt den g-Wert
  • Radius und Drehzahl n bei einer Kreisbewegung: a= 2·pi·r·n/r -> geteilt durch 10 gibt den g-Wert

Zum Beispiel ist die mindestens auftretende Bremsbeschleunigung [in m/s²] ist also gleich dem Quadrat der Aufprallgeschwindigkeit [in m/s] geteilt durch das Doppelte der Bremsstrecke [in m][13].

g-Kräfte bei einem leichten Hammerschlag


Schlägt man mit einem Hammer auf einen Nagel, so kann man über die Eindringtiefe des Nagels und die Geschwindigkeit des Hammers die g-Kraft abschätzen, die auf Hammer und Nagel wirkte. Lässt man einen Hammer aus etwa 50 cm Höhe frei auf den Nagel fallen (man kann ihn dabei mit der Hand etwas führen), so dauert der Fall etwa 0,317 Sekunden (mit s=½at²). Nach dieser Zeit hat er dann eine Geschwindigkeit von etwa 3,17 m/s, oder rund 3 m/s.

MERKSATZ:

9.0 Ein normaler Hammerschlag kann Kräfte von zum Beispiel 45g ergeben.

Je nach Härte des Holzes und Dicke des Nagels dringt der Nagel dann weniger oder mehr tief ins Holz ein. Eine Eindringtiefe von etwa 1 cm oder 0,01 m scheint für einen dünnen Nagel in weichem Holz realistisch. Damit kommt man über die Formel a=v²/(2s) auf g-Kräfte von mindestens 45g. Das liegt in der Größenordnung der Selbstversuche von Major John Paul Stapp mit seinen Raketenschlitten.[8]

g-Kräfte beim Schaukeln


Auch für eine normale Kinderschaukel kann man die g-Kräfte berechnen. Als Länge der Schaukel scheinen zwei Meter vernünftig. Als maximale Auslenkung α von der Ruhelage erscheinen 50° nicht zu hoch gegriffen. Damit kommt man mit Hilfe von Trigonometrie auf eine maximale Höhe der Schaukelbewegung von 0,47 Metern oder rund 0,5 m über dem Ruhepunkt. Das gibt eine potentielle Energie von m·g·h und diese gleichgesetzt mit der kinetischen Energie ½mv² eine Geschwindigkeit von v = √(2·g·h) im Tiefpunkt der Bewegung. Im Beispiel wäre das eine Geschwindigkeit von grob gerundet 3 m/s. Über die Formel für die Zentrifugalbeschleunigung a=v²/r erhält man mit v=3 m/s und r=2m einen Wert von 4,5 m/s oder rund 0,45g. Im Tiefpunkt des Schaukelns spürt man also einen g-Wert von rund 1,45g. Wie beim Start einer Rakete addiert man auch hier die Kräfte der Bewegung zur bereits herrschenden Schwerkraft hinzu. Man kann den Rechengang zu einer einfachen Formel zusammenfassen:

MERKSATZ:

9.0 Die maximale g-Kraft einer Schaukel auf der Erde ist gleich 1+2·(1-cosα). Damit ist 3g der maximal mögliche Wert, nämlich für eine anfängliche Auslenkung von 90°.

Diese Formel ist bemerkenswert, denn in ihr hat sich die Länge der Schaukel weggekürzt. Das heißt, dass die maximalen g-Kräfte im tiefsten Punkt der Schaukel nicht von der Länge der Schaukel abhängen. Selbst bei einer 100 Meter langen Schaukel[19], können 3g nicht überschritten werden.

Die 1 vor dem Pluszeichen bildet die immer herschende Fallbeschleunigung der Erde an ihrer Oberfläche ab. Der Term 2·(1-cosα) steht für die Zentrifugalbeschleunigung im tiefsten und damit schnellsten Punkt des Schaukelns bei einer anfänglichen Auslenkung von α. Im tiefsten Punkt der Schaukelbewegung wirkt die Beschleunigung in dieselbe Richtung wie die Erdanziehungskraft. Daher kann man den Wert zur 1 addieren. Auch ist dort die Geschwindigkeit der Schaukel wegen der vollständigen Umwandlung der potentiellen in kinetische Energie am größten und damit auch die Zentrifugalbeschleunigung. Damit kommt man für eine Schaukel mit einer Auslenkung von etwa 80° auf einen g-Wert von etwa 2,7g.

g-Kräfte bei einer Salatschleuder


Klassische Salatschleudern drehen sich rund 400 bis 600 mal in jeder Minute um sich selbst. Nimmt man den Wert von 600 U/min, dann sind das 10 Umdrehungen in jeder Sekunde. Nimmt man einen Radius von 10 cm oder 0,1 m an, so kommt man damit auf eine Fliehkraft von 360 m/s² oder rund 36g[14]. Das liegt wieder im Bereich der Versuche mit abgebremsten Raketenschlitten.

MERKSATZ:

11.0 Auch normale Salatschleudern kommen auf Kräfte von etwa 36g.

Mit einer Salatschleuder hat man nun ein leicht handhabbares Versuchsgerät, um die Wirkung solcher g-Kräfte zu untersuchen[15]. Man könnte einen feuchten Schwamm damit entwässern. Damit könnte man abschätzen, wie stark Flüssigkeiten aus Körpergewebe geschleudert werden. Zur physikalischen Berechnung siehe auch Salatschleuder ↗

Zusammenfassende Beispielwerte für g-Kräfte


Von g-Kräften spricht man meist, wenn es um die Wirkung starker Beschleunigungen oder Verzögerungen auf den menschlichen Körper geht. Der Begriff ist üblich in der Fliegerei und der Raumfahrt.

  • 1,5g Formel-1 Fahrer beim Start[20]
  • 3,0g Maximalwert für eine Schaukel
  • 3,5g Katapultstart von Kampfflugzeugen[9]
  • 4,0g Start einer Raumfähre[5]
  • 5,0g Formel-1 Fahrer in Kurven[20]
  • 6,0g Kurzfristig bei Achterbahnen[20]
  • 7,2g Wiedereintritt nach einem Mondflug[7]
  • 9,0g Kampfpiloten[9]
  • 45g leichter Hammerschlag
  • 46g Selbsttest mit Raketenschlitten[8]
  • 180g Aufprall eines Rennfahrers auf eine Betonwand[1]

In der Physik ist der Begriff der g-Kraft eher unüblich. Dort gibt man direk t die Beschleunigung üblicherweise m/s² an. Dabei gilt: der Wert der g-Kraft mal 10 gerechnet gibt den Wert der Beschleunigung in m/s². Beispiele dazu stehen im Artikel Beschleunigungen ↗

Körperliche Effekte bei unterschiedlichen g-Kräften


Wie viel g ein Mensch aushalten kann, beziehungsweise welche Effekte dabei auftreten hängt nicht nur von der Stärke der g-Kräfte ab sondern auch von der Richtung. Vor allem wichtig ist, ob das Blut vom Kopf weg (positive g-Werte) oder zum Kopf hin (negative g-Werte) strömt.[21]

Positive g-Werte


  • In gerader oder sitzender Haltung nimmt die Geschwindigkeit des Körpers in Richtung Kopf zu.
  • Blut hängt aufgrund seiner Trägheit etwas hinterher, es sackt Richtung Beine ab.
  • Blut wird dadurch vor allem aus dem Kopf abezogen, dort weniger verfügbar.
  • Ab etwa 3g kann ein untrainierter Mensch aus sitzender Haltung nicht mehr aufstehen
  • Nach einigen Sekunden bei 2g bis 4g gibt es Sehstörungen.
  • Nach einigen Sekunden ab 5g bis 6g droht Bewusstlosigkeit weil kein Blut mehr in das Gehirn gelangt.

Negative g-Werte


  • In gerader oder sitzender Haltung nimmt die Geschwindigkeit des Körpers in Richtung Füße zu.
  • Blut hängt aufgrund seiner Trägheit etwas hinterher, es sammelt sich mit Druck im Kopf an.
  • -1 (Kopfstand) ist problemos, aber kurz darüber schon schmerzhaft.
  • Bei -3g droht der Redout-Effekt (Blut staut sich sichtbar in den Augen)
  • Ab 5g Gefahr der Bewusstlosigkeit sowie Hirnblutungen durch platzende Adern.

Gegenmaßnahmen


Kampfpiloten und Astronauten können den gefährlichen Auswirkungen hoher g-Kräfte etwas entgegen wirken. Dazu dienen zum Beispiel spezielle Atemtechniken und Anspannung von Muskeln. Auch gibt es Druckanzüge, die etwa auf die Beine pressen, um das Blut sich dort nicht ansammeln zu lassen.

Fußnoten


  • [1] Im Jahr 1977 prallte der englische Rennfahrer David Purley bei einem Autorennen in den Niederlanden mit einer Geschwindigkeit von 173 km/h auf eine Betonwand. Die Geschwindigkeit wurde über eine Strecke von nur 66 Zentimetern vollständig auf 0 km/h abgebaut. Dabei trat für kurze Zeit eine negative Beschleunigung (Verzögerung) von fast 1800 m/s² oder rund 180g auf. Purley erlitt mehrere Knochenbrüche. Laut Guiness-Buch der Rekorde zählt das zu den höchsten nachgewiesenen und von Menschen überlebten Beschleunigungen. Siehe auch g-Kraft ↗
  • [2] Es lohnt sich, lange über diese Axiom Newton nachzudenken, insbesondere dass auch der Umkehrschluss gilt: beobachtet man nämlich, dass ein Körper seine Geschwindigkeit nicht ändert, so kann man daraus schließen, dass die Summe aller von außen auf ihn einwirkenden Kräfte Null ist. Wesentlich ist auch, dass es um die resultierenden Kräfte geht. Das ist näher erklärt im Artikel Erstes Newtonsches Axiom ↗
  • [4] Bei Profispielern verlässt der Golfball mit bis zu 68 Metern pro Sekunde Geschwindigkeit das kleine Tee. Siehe dazu auch Golfballparabel ↗
  • [6] Der ehemalige Astronaut Tom Jones (geboren 1955) schreibt zur Beschleunigung beim Wiedereintritt: "On shuttle reentry, the forces put on the body as the craft decelerated through the atmosphere were only 1.7 Gs, and usually just a normal 1 G or so. But the peak deceleration lasted for about ten minutes, quite a strain to withstand after living in weightlessness for a couple of weeks." In: Tom Jones: Ask the Astronaut: Which is more fun, the ascent into orbit or the reentry? Smithsonian Air & Space Magazine. April 30, 2016.
  • [7] Beim Wiedereintritt von Apollo-Kapseln aus einen niederen Erdorbit lagen die Werte bei etwa 3g. Beim Wiedereintritt nach einem Mondflug lagen die Werte üblicherweise über 6g und in einem Fall auch bei bis zu 7,19g. In: Biomedical Results of Apollo. Zusammengestellt vom Lyndon B. Johnson Space Center. Herausgegeben von der NASA im Jahr 1975 unter der Nummer SP-368. Dort die Seiten 134 und 135. Online: https://ntrs.nasa.gov/api/citations/19760005580/downloads/19760005580.pdf
  • [8] Sebastian Hollstein: Der menschliche Crashtest-Dummy: Was hält unser Körper aus? Die Antwort suchte Major John Paul Stapp mit seinem Raketenschlitten. Von mehr als 1000 Stundenkilometern bremste er auf null - in anderthalb Sekunden. In: Spektrum der Wissenschaft. Serie: Kuriose Experimente am Menschen. Oktober 2019. Über die Formel v=at kann man die Beschleunigung a berechnen und erhält etwa 185 m/s² oder rund 19g. Der Wikipedia-Artikel zu Paul Stapp führt aus, dass Stapp kurzzeitig Bremskräften von gut 46g ausgesetzt und über gut eine Sekunde ununterbrochen 25g wirkten. Siehe auch: https://de.wikipedia.org/wiki/John_Paul_Stapp
  • [9] Beim Katapultstart einer Hornet (Kampfjet) wird das Flugzeug in etwa 2 Sekunden auf einer Strecke von etwa 94 Metern von 0 auf über 140 Knoten, das sind fast 300 km/h beschleunigt. Dabei treten g-Kräfte von 3 bis 3,5 auf: "Naval pilots flying from aircraft carriers feel the extremes of this type of G force. During a catapult launch, the aircraft accelerates to 160-plus mph in just under two seconds". In: Acceleration in Aviation. Federal Aviation Administration. OK-21-0375 12/14/2021. Als Beispiel dazu siehe McDonnell Douglas F-18 Hornet ↗
  • [10] Bis zu 9g für Kampfpiloten: "A pilot in a steep turn may experience forces of acceleration equivalent to many times the force of gravity. This is especially true in military fighter jets and high-performance, aerobatic aircraft where the acceleration forces may be as high as 9 Gs." In: Acceleration in Aviation. Federal Aviation Administration. OK-21-0375 12/14/2021. Die hier wirkende Kraft ist die Fliehkraft ↗
  • [11] Die Formel v=at gilt für gleichmäßig beschleunigte Bewegung. Bei einem Unfall ist der Bremsvorgang mit großer Wahrscheinlichkeit nicht gleichförmig. Die Formel liefert damit aber auf jeden Fall einen Mindestwert für die g-Kraft. Siehe auch v=at ↗
  • [12] Auch die Formel s=½at² gilt nur für gleichmäßig beschleunigte Bewegungen. Siehe mehr unter s=½at² ↗
  • [13] Als der Rennfahrer Purley mit 173 km/h oder rund 48 m/s auf eine Betonwand prallte, wurde er über eine Strecke von 0,66 Metern gebremst. Nach der Formel a=v²/(2s) ergibt dies eine Beschleunigung a von rund 1745 m/s² oder rund 180g. Das ist genau der Wert, der auch in der Literatur angegeben wird.
  • [14] Zur Salatschleuder: bei einem Radius von 10 cm ergibt das über die Formel für den Kreisumfang eine Strecke von etwa 0,6 Meter für eine Kreisbewegung. Da die Schüssel 10 Umdrehungen pro Sekunde macht, sind das 6 Meter pro Sekunde. Über die Formel a=v²/r kommt man dann auf eine Beschleunigung von rund 360g.
  • [15] Aber bitte nicht mit Tieren: was mir schon immer offensichtlich schien, dass nämlich auch scheinbar einfach gebaute Tiere ein reiches Gefühlsleben haben könnten, scheint die Forschung zu bestätigen. Hummeln scheinen zu spielen, Spinnne zu träumen. Und um Angst zu spüren, braucht man nicht viel IQ. Siehe dazu auch Speziesismus ↗
  • [16] In einem Graphen sind die g-Kräfte als Funktion der Zeit für den Aufstieg einer Saturn-V Rakete aufgetragen. Bei etwa 140 bis 150 Sekunden nach dem Start werden fast 5g erreicht. Zum Zeitpunkt t=0 ist die g-Kraft mit genau 1 angegeben (y-Achsenabschnitt). In: Biomedical Results of Apollo. Zusammengestellt vom Lyndon B. Johnson Space Center. Herausgegeben von der NASA im Jahr 1975 unter der Nummer SP-368. Dort die Seite 134. Online: https://ntrs.nasa.gov/api/citations/19760005580/downloads/19760005580.pdf
  • [17] Im Jahr 2024 beispielsweise bot die Firma AirZeroG einen Parabelflug in eine Airbus A310 für 7500 Euro an. Die Flüge starten vom französischen Toulouse aus. Siehe auch Parabelflug ↗
  • [18] In der sogenannten Ballistik spricht man immer dann von einem freien Fall, wenn nur als äußere Kräfte an einem Körper nur die Anziehungskräfte von Himmelskörpern wirken. Damit wäre zum Beispiel ein nach oben geworfener Stein auch während des Aufstiegs im freien Fall, nicht nur beim Herunterkommen. Siehe mehr dazu im Artikel Freier Fall ↗
  • [19] Seit dem Jahr 2020 soll die höchste Schaukel der Welt in China stehen: "The world's tallest swing has just opened over a 2,300-foot-tall cliff in China. The extreme ride is 328 feet [ziemlich genau 100 Meter] tall, roughly the equivalent of a 30-story building […] The swing can catapult tourists over the cliff edge at a top speed of 80 miles per hour [etwa 130 km/]." In: World's tallest swing opens in China. 25ter Juli 2020. CGTN. Geht man von einer maximalen Auslenkung von 90 Grad aus, so liegt die Starthöhe der Schaukel bei 100 Metern. Über ein Gleichsetzen von potentieller und kinetischer Energie (mgh=½mv²), kommt man dann mit g=10 m/s² zu einer maximalen Geschwindigkeit von 162 km/h. Geht man von einer geringeren Auslenkung als 90° aus oder berücksichtigt man den Luftwiderstand, so erscheint die Angabe von 130 km/h aus dem Artikel der chinesischen Zeitung realistisch. Aber auch hier liegen die g-Kräfte bei maximal 3g.
  • [20] Klaus Hannemann: Wieviel g kann ein Mensch aushalten? Max-Planck-Institut für Dynamik und Selbtorganisation. 2009. Dort findet man: Formel-1 Fahrer beim Start etwa 1g bis 1,5g und in Kurven bis 5g; Passagierflugzeuge in üblichen Manövern maximal 1,5g; Astronauten in einer Erdumlaufbahn 0g; Sojus-Kapsel beim Wiedereintritt bis 10g; Achterbahnen bis 6g. Online: https://www.ds.mpg.de/131983/18
  • [21] Klaus Hannemann: Wieviel g kann ein Mensch aushalten? Max-Planck-Institut für Dynamik und Selbtorganisation 2009: ab etwa 3g kann ein untrainierter Mensch aus sitzender Haltung nicht mehr aufstehen; Nach einigen Sekunden Beschleunigung mit dem Kopf nach vorne bei 2g bis 4g Sehstörungen und bei 5g bis 6g Bewusstlosigkeit weil kein Blut mehr in das Gehirn gelangt. Bei Beschleunigung mit den Füßen nach vorne (negative Beschleunigung): -1 (Kopfstand) ist problemos, aber kurz darüber schon schmerzhaft, bei -3g Redout-Effekt (Blut staut sich sichtbar in den Augen), ab 5g Gefahr der Bewusstlosigkeit sowie Hirnblutungen durch platzende Adern. Online: https://www.ds.mpg.de/131983/18