Beispiele
Als Achse bezeichnet man oft eine feste Linie um die herum sich etwas anderes dreht oder angeordnet ist. Hier stehen kurz aufgelistet einige Beispiele. => Ganzen Artikel lesen …
… es gibt mehrere, siehe unter => Achsen
 Wachsen
Wachsen
Mathematik | Physik
Eigentlich: größer, länger oder breiter werden. Daneben gibt es noch weitere Bedeutungen (z. B. mit Wachs einreiben). Diese werden hier kurz vorgestellt. Aus Sicht der Mathematik ist das Thema behandelt unter => Wachstum
 Aachen
Aachen
Stadt
Westlichste Großstadt von Deutschland: die Stadt Aachen zählt rund 240 Tausend Einwohner. Aachen ist berühmt dafür, dass von hier aus Kaiser Karl der Große sein großes Frankenreich regierte. Das war um das Jahr 800 nach Christus. Heute beherbergt Aachen bekannte Hochschulen und ist der Ort vieler weltweit beachteter Veranstaltungen. => Ganzen Artikel lesen …
… siehe unter => x-Achsenabschnitt
… das passt auf f(x)=0, also die => Nullfunktion
Mathematik
Die x- und y-Achsen in kleine Abschnitte einteilen und diese mit Zahlen zu beschriften nennt man die Achsen skalieren. Das ist beim Zeichnen eines Koordinatensystem oft der schwierigste Schritte. => Ganzen Artikel lesen …
… wo ein Graph die x- oder y-Achse schneidet => Achsenabschnitte
es gibt zwei Möglichkeiten:
- => y-Achsenabschnitt bestimmen
… siehe unter => y-Achsenabschnitt von Geraden bestimmen
… siehe unter => y-Achsenabschnitt bestimmen
x und y
Achsenabschnitte sind die Orte auf einer Achse des Koordinatensystems, an denen ein Funktionsgraph die Achse schneidet oder berührt. Hier stehen Beispiele dazu. => Ganzen Artikel lesen …
es gibt mehrere Möglichkeiten:
- => y-Achsenabschnitt bestimmen
… in der Vektorrechnung => Achsenabschnittsform der Ebene
 Achsenabschnittsform der Ebene
Achsenabschnittsform der Ebene
Aufbau
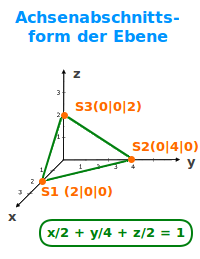
x/xo + y/yo + z/zo = 1: die Zahlen für xo, yo und zo sind die Schnittpunkte mit den 3 Koordinatensachsen. Damit kann man sich die Ebene leicht anschaulich vorstellen. => Ganzen Artikel lesen …
Lineare Funktion
x:a+y:b=1 ist die sogenannte Abschsenabschnittsform einer Geraden, das heißt des Graphen einer linearen Funktion. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Lineare Funktion
x/a+y/b=1 ist die sogenannte Abschsenabschnittsform einer Geraden [1] mit dem a als x-Achsenabschnitt und dem b als y-Achsenabschnitt. Die Gerade ist hier gedeutet als eine lineare Funktion. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Vektorrechnung
Achsenabschnittsform in Allgemeine Normalenform: hier wird kurz die Grundidee vorgestellt, wie man eine gegebene Form oder Darstellungsweise einer Ebene in eine gesuchte andere Form der Ebene umwandelt. => Ganzen Artikel lesen …
Vektorrechnung
Achsenabschnittsform in Hessesche Normalenform: hier wird kurz die Grundidee vorgestellt, wie man eine gegebene Form oder Darstellungsweise einer Ebene in eine gesuchte andere Form der Ebene umwandelt. => Ganzen Artikel lesen …
Vektorrechnung
x/xo + y/yo + z/zo = 1 ist der Bauplan für die sogenannte Achsenabschnittsform und ax+by+cz=d ist der Bauplan für die sogenannte Koordinatenform. Beide Formen sind gedanklich eng miteinander verbunden. Hier stehen zwei Möglicheiten, wie man die Achsenabschnittsform in die Koordinatenform umwandeln kann. => Ganzen Artikel lesen …
Vektorrechnung
x/8+y/8+z/4 = 1 ist eine Ebene in der sogenannten Achsenabschnittsform. Dieselbe Ebene kann man auch in der Parameterform mit Stütz- und Richtungsvektoren angeben. Hier ist die Umwandlung kurz mit einem Zahlenbeispiel erklärt. => Ganzen Artikel lesen …
Vektorrechnung
x/8+y/8+z/4=1 ist eine typische Gleichung für eine Ebene in Achsenabschnittsform. Dieselbe Ebene geschrieben in Punkt-Normalenform (X-p)·n=0 ist mit Zahlen ausgeschrieben (X-(4|4|0))·(1|1|2)=0. Hier ist die Umwandlung kurz vorgestellt. => Ganzen Artikel lesen …
Wo ein Funktionsgraph eine der Achsen schneidet
Ein Funktionsgraph kann sowohl die x-Achse als auch die y-Achse schneiden. Diese Schnittepunkte nennt man Achsenschnittpunkte. Der Schnittpunkt der Koordinatenachsen selbst nennt man den Koordinatenursprung (wenn dort alle Koordinatenwerte Null sind). => Ganzen Artikel lesen …
x, y, z
Ein Funktionsgraph, eine Ebene oder geometrische Figuren aber auch die Koordinatenachsen untereinander können Achsenschnittpunkte haben. Hier stehen einige Beispiele. => Ganzen Artikel lesen …
Anleitung
Hier steht eine Schritt-für-Schritt Anleitung für das Achsenspiegeln in der Geometrie. Am Ende ist das Spiegeln von Funktionsgraphen kurz erklärt. => Ganzen Artikel lesen …
… schmetterlingsartig an eine Linie => Achsenspiegeln
 Achsenspiegelung
Achsenspiegelung
Übersicht
Als Achsenspiegelung bezeichnet man meist die Spiegelung einer Figur an einer Achse innerhalb einer zweidimensionalen Fläche (z. B. auf einem Zeichenblatt). In der Geometrie oder mit Funktionsgraphen: bei einer Achsenspiegelung wird irgendetwas an einer Achse, das heißt einer geraden Linie, gespiegelt. Hier stehen einige wichtige Fälle einer Achsenspiegelung. => Ganzen Artikel lesen …
 Achsensymmetrie
Achsensymmetrie
Schmetterlingsartig
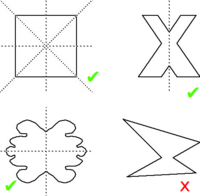
Achsensymmetrie heißt, dass man eine Figur wie zwei Schmetterlingsflügel nahtlos entlang einer Linie falten könnte. Der Begriff kommt vor allem vor in der Geometrie und der Funktionenlehre. Beides wird hier kurz vorgestellt. => Ganzen Artikel lesen …
… meint sinngemäß dasselbe wie => Punktsymmetrie als Alogismus
… z. B. wie f(x)=Siehe unter => Achsensymmetrie von Graphen
… an der y-Achse gespiegelt, mehr unter => Achsensymmetrie von Graphen
… für Funktion => Achsensymmetrie von Graphen
… Schmetterlingssymmetrie, mehr unter => Achsensymmetrie von Graphen
… Schmetterlingssymmetrie, mehr unter => Achsensymmetrie von Graphen
 Achsenymmetrie in der Geometrie
Achsenymmetrie in der Geometrie
Definition
Achsensymmetrie gibt es für Körper (3D) und flache Figuren (2D). Wenn das Gesamtgebilde schmetterlingsartig ist, liegt Achsensymmetrie vor. Exakt: Eine Figur ist achsensymmetrisch, falls es eine Gerade g gibt, so dass es zu jedem Punkt P der Figur einen weiteren (eventuell mit P identischen) Punkt P' der Figur gibt, so dass die Verbindungsstrecke [PP'] von dieser Geraden rechtwinklig halbiert wird. Das ist hier näher erläutert. => Ganzen Artikel lesen …

