A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 9 Ω
Das Banner der Rhetos-Website: zwei griechische Denker betrachten ein physikalisches Universum um sie herum.

Zahlenarten

Übersicht

© 2016 - 2025


Basiswissen｜ ℕ: Natürliche Zahlen｜ ℤ: Ganze Zahlen｜ ℝ: Reelle Zahlen｜ ℚ: Rationale Zahlen｜ ℂ: Komplexe Zahlen｜ Irrationale Zahlen｜ *R: Infinitesimale Zahlen｜ Hyperreelle Zahlen｜ Surreale Zahlen｜ Transzendente Zahl｜ Bruchzahlen｜ Kommazahlen｜ Echte Kommazahlen｜ Gleitkommazahlen｜ Festkommazahlen｜ Dezimalzahlen｜ Große Zahlen｜ Negative Zahlen｜ Gemischte Zahlen｜ Normale Zahlen｜ Konstante Zahlen｜ Variable Zahlen｜ Zufallszahlen｜ Arabische Zahlen｜ Römische Zahlen｜ Binäre Zahlen｜ Oktale Zahl｜ Hexadezimalzahl｜ Duodezimalzahl｜ Imaginäre Zahlen｜ Schnapszahl｜ Palindromzahl｜ Spiegelzahl｜ Gegenzahl｜ Kardinalzahl｜ Ordinalzahl｜ Fußnoten


Basiswissen


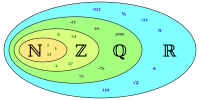
ℕ, ℤ, ℝ, ℚ und ℂ sind die wichtigsten Zahlenarten in der Schulmathematik. Daneben gibt es noch weitere besondere Zahlenarten wie normale Zahlen (die sehr selten sind), die eher inoffiziellen Kommazahlen sowie auch exotische Formen wie surreale und hyperreelle Zahlen. Hier sind 32 solcher Zahlenarten kurz vorgestellt.



Bildbeschreibung und Urheberrecht
Die Zahlenarten als Untermengen voneinander. Man beachte, dass die jeweils größere Menge immer auch alle Elemente der enthaltenen Menge in sich hat. © Mortalmoth ☛


ℕ: Natürliche Zahlen


  • Natürlich nennt man die Zahlen 1; 2; 3; 4 und so weiter.
  • Die natürlichen Zahlen gehen unendlich weiter.
  • Es sind sozusagen auch die Grundschulzahlen.
  • Man nennt sie auch die Zählzahlen.
  • Die 0 gehört normalerweise nicht dazu.

ℤ: Ganze Zahlen


  • Das sind Zahlen wie -3; -2; -1; 0; 1; 2; 3 und so weiter.
  • Ganze Zahlen kann man in Dezimalform immer ohne Komma schreiben.
  • Keine ganzen Zahlen sind zum Beispiel 2,5 oder 0,99.

ℝ: Reelle Zahlen


  • Das sind alle Zahlen, die man irgendwo auf der Zahlengeraden schreiben kann.

ℚ: Rationale Zahlen


  • Das sind alle Zahlen, die man als Bruch schreiben kann.
  • Eine Bedingung ist dabei: der Zähler und Nenner müssen ganze Zahlen sein.

ℂ: Komplexe Zahlen


  • Das sind Zahlen, die nicht auf der Zahlengeraden liegen müssen.
  • Sie liegen sozusagen oberhalb oder unterhalb der Zahlengeraden.
  • Die 5 als komplexe Zahl wäre zum Beispiel: 5+0i

Irrationale Zahlen


  • Das sind Zahlen, die man nicht als Bruch schreiben kann.
  • Rational heißt hier so viel wie: als Bruch (ratio) schreibbar.
  • Bekannte irrationale Zahlen sind zum Beispiel Pi oder e.

*R: Infinitesimale Zahlen


  • Das sind Zahlen, von denen eine Summe nie größer sein kann als 1.
  • Diese Zahlen wurden künstlich über die Mengenlehre konstruiert.
  • Sie dienen vor allem rein theoretischen Interessen.

Hyperreelle Zahlen


  • Sie liegen näher an einer reellen Zahl, als jede andere reelle Zahl.
  • Hyperreelle Zahlen spielen in der Schulmathematik keine Rolle.

Surreale Zahlen


  • Surrealle Zahlen enthalten die reellen und die hyperreellen Zahlen.
  • Sie können selbst als konkrete Einzelzahl auch unendlich große Werte annehmen.

Transzendente Zahl


  • Eine transzendente Zahl ist immer irrational.
  • Der Begriff wird nicht einheitlich verwendet.

Bruchzahlen


  • Dieser Begriff wird nicht einheitlich verwendet.
  • Man kann darunter die rationalen Zahlen verstehen.
  • Denn: rationale Zahlen kann man immer als Bruch schreiben.
  • Man kann mit dem Wort aber auch eine Zahl in Bruchdarstellung meinen.
  • Also: eine Zahl sichtbar mit Bruchstrich als Bruch geschrieben.

Kommazahlen


  • Auch dieser Begriff wird nicht einheitlich verwendet.
  • Er wird oft gleichbedeutend mit Dezimalzahl verwendet.
  • Man will damit andeuten, dass eine Zahl mit Komma geschrieben ist.
  • Man schreibt dann zu Eindeutigkeit besser: eine Zahl mit sichtbarem Komma

Echte Kommazahlen


  • Damit meint man Zahlen, die mit einem sichtbaren Komma geschrieben sind.
  • Die 4 und die 4,0 sind beide dieselbe Zahl, nur unterschiedlich dargestellt.
  • Man könnte sagen, dass die 4 eine Kommazahl mit unsichtbarem Komma ist.

Gleitkommazahlen


  • Gleit- oder Fließkommazahlen spielen in der Informatik eine Rolle.
  • Sie sind spezielle Annäherung für reelle Zahlen.
  • 4,1E3 oder 4,1·10³ sind typische Beispiele.

Festkommazahlen


  • Bei einer Festkommazahl ist die Anzahl Ziffern vor und nach dem Komma festgelegt.
  • Man kann zum Beispiel festlegen: vor dem Komma 2 und nach dem Komma 3 Ziffern.
  • Festkommazahlen kommen im Zusammenhang mit Rechenmaschinen und Computern vor.

Dezimalzahlen


  • Man sagt besser: eine Zahl in Dezimaldarstellung
  • Zu diesen Zahlen gehören zum Beispiel: -4; 0; 15; 24,9999
  • Eine Zahl in Dezimaldarstellung darf ein Komma haben - muss es aber nicht.

Große Zahlen


  • "Große Zahlen" ist ein häufiger Titel von Kapiteln in Schulbüchern.
  • Damit sind oft Zahlen gemeint wie 10000000 oder 45250000000000000.

Negative Zahlen


  • Das sind alle Zahlen, die kleiner sind als die Null.
  • Die 0 selbst gehört nicht zu den negativen Zahlen.
  • Eine negative Zahl schreibt man immer mit einem - als Vorzeichen.

Gemischte Zahlen


  • Zum Beispiel zweieinhalb oder kurz geschrieben: 2½
  • 2½ meint: zwei mal die 1 und dann ein Halbes noch dazu.
  • Gemischte Zahlen sind oft sehr anschaulich.

Normale Zahlen


  • In der Mathematik ist das Wort normale Zahl definiert.
  • Normale Zahlen sind tatsächlich extrem selten und schwer konstruierbar.
  • Sie sind also genau das Gegenteil von dem was man für normal hält.

Konstante Zahlen


  • Konstant nennt man Zahlen, die immer gleich bleiben sollen.
  • Die Kreiszahl Pi zum Beispiel ist eine Konstante.
  • Sie soll gerundet immer den Wert 3,14 haben.

Variable Zahlen


  • Variable nennt man Zahlen, die sich verändern dürfen.
  • In der Funktionsgleichung f(x) = 4·x-5 ist das x eine typische Variable.
  • Variablen treten als Buchstaben in Formeln, Funktionen und Termen auf.

Zufallszahlen


  • Zahlen, die in einer Reihenfolge nacheinander erscheinen, ...
  • für die man aber keiner Regelmäßigkeit erkennen kann.

Arabische Zahlen


  • Das sind die uns bekannten Schreibweisen wie 425 oder 10000.
  • Die 0; 1; 2; 3; 4; 5; 6; 7; 8 und 9 nennt man arabische Ziffern.

Römische Zahlen


  • Die I für die 1 oder die IX für die 9 sind bekannte Beispiele.
  • Römische Zahlen verwendet man oft für Nummerierungen.

Binäre Zahlen


  • Auch duale Zahlen gennant: 111 ist die 7 und 1000 wäre die 8.
  • Binäre Zahlen sind für Computerwissenschaftler nützlich.

Oktale Zahl


  • Eine Zahl im 8er-System:
  • Oktalzahlen sind vor allem für Informatiker interessant.
  • Man kann sie optisch nicht von Dezimalzahlen unterscheiden.

Hexadezimalzahl


  • Eine Zahl im Sechzehnersystem:
  • Man erkennt sie oft daran, dass sie ein A, B, C, D, E oder F enthalten.
  • Die Zahl 1A wäre die 11 als Dezimalzahl.

Duodezimalzahl


  • Eine Zahl im Zwölfersystem.
  • Das Zwölfersystem lebte bruchstückhaft in Begriffen wie Dutzend oder Schock.

Imaginäre Zahlen


  • Diese sind eng verwandt, aber begrenzter als die komplexen Zahlen.
  • Der Grundgedanke ist: i² soll genau -1 ergeben.
  • Damit hätte man eine Wurzel für die Zahl -1

Schnapszahl


  • Eine Zahl, die nur aus gleichen Ziffern besteht, z. B.: 44444

Palindromzahl


  • Eine Zahl, die umgekehrt geschrieben ist zu einer anderen:
  • Beispiel: die 123456 ist ein Palindrom von 654321

Spiegelzahl


  • Meint dasselbe wie Palindromzahl:
  • Die Ziffern sind rückwärts geschrieben zu einer anderen Zahl.

Gegenzahl


  • Dieselbe Zahl nur mit anderem Vorzeichen:
  • Die -8 ist die Gegenzahl von der 8.

Kardinalzahl


  • Die 4 im Sinne: sie besaß insgesamt vier Häuser.
  • Eine Zahl, die sagt, wie viel man von etwas hat.
  • Dies ist keine Zahlenart oder Darstellung, sondern eine Deutung.
  • Wenn man sagt, man sehe 4 Amseln, dann ist die 4 hier kardinal verwendet[1][2].
  • Zur Abgrenzung: die 4te Amsel wäre die Deutung als Ordinalzahl.

Ordinalzahl


  • Die 4 im Sinne: die vierte Person in der Wartschlange.
  • Eine Zahl, die sagt, wo man in einer Reihenfolge steht.
  • Dies ist keine Zahlenart oder Darstellung, sondern eine Deutung.
  • Wenn man sagt, man stehe an vierter Stelle ist das die ordinale Zahldeutung[2].

Fußnoten


  • [1] Katja Rochmann, Michael Wehrmann: Bloß kein minus … lieber plus. Ein Lehr- und Lernbuch für den Grundschulstoff. Herausgegeben vom Arbeitskreis des Zentrums für angewandte Lernforschung. Osnabrück. 2009. ISBN: 978-300-028253-9. Dort wird ab Seite 19 die Kardinalzahl als die eigentliche Zählzahl behandelt, die Art von Zahl für "Anzahlen".
  • [2] Michael Wehrmann: Qualitative Diagnostik von Rechenschwierigkeiten im Grundlagenbereich Arithmetik. Verlag Dr. Köster. Berlin. 2. Auflage. 2009. ISBN: 978-3-89574-474-7. Dort spielen die Konzept der Kardinal- und Ordinalzahlen an vielen Stellen eine Rolle. Es ist empfohlen den Begriff dort im Register nachzuschlagen.