ℜ
Physik Chemie Grundschule Mathematik I Mathematik II Wissen
Kurze Worte Worte nach Alter Terme Rechner
Mathfeed Physfeed Philfeed
Das Lexikon Die Mission Die Autoren Copyright Impressum
Physik 5-10 Physik 11-13 Chemie 5-13 Mathe 5-8 Mathe 9-10 Mathe 10-13
☰
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 9 Ω
Das Banner der Rhetos-Website: zwei griechische Denker betrachten ein physikalisches Universum um sie herum.

Ungerade Funktion

Definition

© 2016 - 2025


Basiswissen · Beispiele für ungerade Funktion · Wie erkennt man eine ungerade Funktion? · Ist jede ungerade Funktion auch punktsymmetrisch? · Ist jede punktsymmetrische Funktion auch eine ungerade Funktion? · Wie kann man einen Graphen punktspiegeln an (0|0)? · 1. Methode: Punktspiegeln über x- und y-Achsen · 2. Methode: Punktspiegelung über die Stecknadel-Methode · Woher kommt der Name? · Gibt es auch eine gerade Funktion? · Fußnoten


Basiswissen


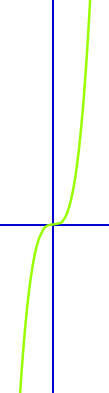
Eine Funktion deren Graph punktsymmetrisch zum Ursprung (0|0) eines Koordinatensystems ist nennt man ungerade[1]. Das ist hier näher mit Beispielen definiert.



Bildbeschreibung und Urheberrecht
f(x) = x³☛


Beispiele für ungerade Funktion



Wie erkennt man eine ungerade Funktion?



Ist jede ungerade Funktion auch punktsymmetrisch?


Ja, eine ungerade Funktion ist immer punktsymmetrisch zum Punkt (0|0) eines Koordinatensystems und damit auch punktsymmetrisch an sich. Punktsymmetrie heißt für Graphen, dass es irgendeinen Punkt gibt, zu dem der Graph symmetrisch ist. Die ungerade Funktion ist ein Sonderfall für eine punktsymmetrische Funktion ↗

Ist jede punktsymmetrische Funktion auch eine ungerade Funktion?


Nein, eine Funktion kann zum Beispiel punktsymmetrisch zum Punkt (2|2) sein. Dann ist sie an sich punktsymmetrisch, aber nicht zum Koordinatenursprung (0|0). Punktsymmetrie allgemeine heißt an sich nur, es gibt irgendeinen Symmetriepunkt ↗

Wie kann man einen Graphen punktspiegeln an (0|0)?


  • Dazu gibt es zwei praktisch-anschauliche Methoden.
  • Man kann ihn schrittweise über die x- und y-Achse spiegeln.
  • Oder man dreht ihn einfach um 180° um den Punkt (0|0).
  • Beide Verfahren führen immer zum selben Ergebnis.

1. Methode: Punktspiegeln über x- und y-Achsen


  • Ein gegebener Graph mit Funktionsgleichung soll punktgespiegelt werden.
  • Man nimmt dazu einen beliebigen Punkt auf dem Graphen.
  • Man spiegelt ihn zuerst an der x-Achse.
  • Aus dem Punkt (4|2) wird dann zum Beispiel: (4|-2)
  • Dann spiegel man diesen neuen Punkt an der y-Achse.
  • Aus dem Punkt (4|-2) wird dann der Punkt: (-4|-2)
  • Das mit allen Punkten des Graphen gemacht ergibt eine Punktspiegelung.

2. Methode: Punktspiegelung über die Stecknadel-Methode


  • Man stellt sich die Koordinatenachsen auf den Tisch gezeichnet vor.
  • Der eigentliche Graph (die Kurve alleine) wäre auf Klarsichtfolie gezeichnet.
  • Man sticht gedanklich eine Stecknadel durch die Folie in den Punkt (0|0).
  • Dann dreht man die Folie um 180° (Halbkreis).
  • Dabei sind die x- und y-Achse an der alten Stelle geblieben.
  • Die gedrehte Folien-Kurve ist die punktgespiegelte Funktion.

Woher kommt der Name?


  • Der Name hat nichts mit der Form des Graphen zu tun.
  • Die Graphen dürfen zum Beispiel auch Geraden sein.
  • Der Name kommt von den Exponenten von x her.
  • Bei ganzrationalen Funktionen hat das x immer nur ungerade Exponenten.

Gibt es auch eine gerade Funktion?


Ja, wenn der Graph einer Funktion symmetrisch zu y-Achse ist, dann nennt man diese Funktion gerade. Siehe auch gerade Funktion ↗

Fußnoten