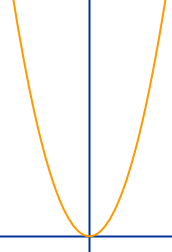
Gerade Funktion
Symmetrie
Basiswissen
Gerade nennt man jede Funktion, deren Graph achsensymmetrisch zur y-Achse ist. Formal gilt dann: f(x) = f(-x). Bei einer ganzrationalen Funktion sind dann auch alle Exponenten von x eine gerade Zahl. das ist hier näher vorgestellt.
Beispiele für gerade Funktionen
Wie erkennt man eine gerade Funktion?
- Über die Gleichung mit der Exponentenregel der Graphensymmetrie ↗
- Am Graphen, der Graph ist achsensymmetrisch zur y-Achse ↗
- Formal über die Bedingung f(x)=f(-x) ↗
Ist jede gerade Funktion auch achsensymmetrisch?
Ja, jede gerade Funktion ist per Definition immer achsensymmetrisch zur y-Achse eines Koordinatensystems. Wie in der Geometrie nennt man auch in der Analysis eine Figur - ein Graph ist eine Figur - genau dann achsensymmetrisch, wenn man für sie irgendeine Symmetrieachse finden kann. Siehe mehr zu dieser Grundgedanken im Artikel Symmetrieachse ↗
Ist jede achsensymmetrische Funktion auch gerade?
Nein, der Graph der Parabel von der Funktion f(x)=(x-2)² ist an sich achsensymmetrisch: die Symmetrieachse ist eine senkrechte Linie durch die Stelle x=2 im Koordinatensystem. Der Graph ist aber nicht achsensymmetrisch zur y-Achse und damit auch nicht gerade. Eine gerade Funktion ist ein Sonderfall für eine achsensymmetrische Funktion ↗
Eine Eselsbrücke für den Namen
- Der Name hat nichts mit der Form des Graphen zu tun.
- Die Graphen müssen insbesondere keine Geraden sein.
- Der Name kommt von den Exponenten von x her.
- Bei ganzrationalen Funktionen hat das x immer nur gerade Exponenten.
- Siehe auch Exponentenregel der Graphensymmetrie ↗
