Gerade und ungerade Funktionen
Symmetrie
Basiswissen
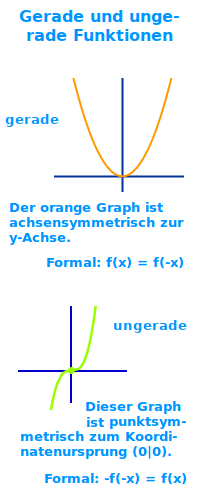
Man nennt eine Funktion gerade, wenn ihr Graph achsensymmetrisch zur y-Achse ist. Der Graph sieht dann oft schmetterlingsartig aus. Man nennt eine Funktion ungerade, wenn ihr Graph punktsymmetrisch zum Ursprung (0|0) des Koordinatensystem ist. Das ist hier ausführlich erklärt.
Gerade Funktion
- Formal schreibt man: f(x) = f(-x)
- Der Graph ist achsensymmetrisch zur y-Achse ↗
- Bei ganzrationalen Funktionen: alle Exponenten von x sind gerade Zahlen ↗
- Mehr unter gerade Funktion ↗
Ungerade Funktion
- Formal schreibt man: f(x) = -f(-x)
- Der Graph ist punktsymmetrisch zum Koordinatenursprung ↗
- Bei ganzrationalen Funktionen: alle Exponenten von x sind ungerade Zahlen ↗
- Mehr unter ungerade Funktion ↗
Die Exponentenregel der Symmetrie von Funktionsgraphen
Wenn alle Exponenten von x gerade sind (-4, -2, 0, 2, 4 etc.), dann ist der Graph der Funktion achsensymmetrisch zur y-Achse. Wenn alle Exponenten von x ungerade sind (-3, -1, 1, 3 etc.), dann ist der Graph der Funktion punktsymmetrisch zum Koordinatenursprung (0|0). Diese Regel gilt für alle - aber auch nur für - ganzrationale Funktionen. Die Regel ist mit Beispielen erklärt im Artikel zur Exponentenregel der Graphensymmetrie ↗
