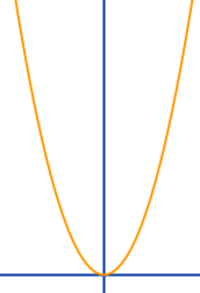
Achsensymmetrie von Graphen
Übersicht
Basiswissen
Achsensymmetrie heißt allgemein: der Graph einer Funktion sieht schmetterlingsartig an einer geraden Linie, der Symmetrieachse, gespiegelt aus. Im engeren Sinn ist die y-Achse (senkrechte Achse) diese Symmetrieachse.
Was meint Achsensymmetrie in der Schulmathematik?
- In der Schulmathematik meint das meistens: zur y-Achse.
- Der Graph ist schmetterlingsartig an der y-Achse gespiegelt:
- Ein x-Wert und seine Gegenzahl haben dann immer den gleichen y-Wert.
- Formal definiert man Achsensymmetrie so: f(x) = f(-x).
- Das ist die Achsensymmetrie im engeren Sinn.
- Siehe auch unter f(x)=f(-x) ↗
- Allgemein gerade Funktion ↗
Was ist Achsensymmetrie im allgemeinen Sinn?
- In der Schulmathematik wird Achsensymmetrie oft nur auf die y-Achse bezogen.
- Man sollte präziser immer sagen: "achsensymmetrisch zur y-Achse".
- Ein Graph kann aber auch symmetrisch zu einer ganzen anderen Achse sein.
- So ist zum Beisiel die Gerade g(x)=2x achsensymmetrisch zu a(x)=-0,5x.
- Zu sagen, dass g(x) nicht achsensymmetrisch ist, ist also falsch.
- g(x) ist zwar nicht achsensymmetrisch zur y-Achse, aber zu a(x).
- Siehe auch Achsensymmetrie ↗
Welche Angabe ist immer wichtig?
- Man sollte immer sagen, worauf man die Symmetrie bezieht.
- Damit vermeidet man Mehrdeutigkeiten.
- Gut: Der Graph ist achsensymmetrisch zur y-Achse.
- Gut: Der Graph ist achsensymmetrisch zur Geraden f(x)=-0,5x.
- Gut: Der Graph ist achsensymmetrisch zur x-Achse.
- Nicht gut: Der Graph ist achsensymmetrisch.
Welche Graphen sind immer achsensymmetrisch zu y-Achse?
- Die Graphen aller konstanten Funktionen,
- die Graphen aller reinquadratischen Funktionen,
- die Graphen aller reinquartischen Funktionen,
- der Graph der einfachen Cosinusfunktion,
- alle Graphen von Betragsfunktionen
- alle Graphen von ganzrationalen Funktionen, ...
- die nur geradzahlige Exponenten haben.
- Siehe auch gerade Funktionen ↗
Was ist die Exponentenregel?
- Sie gilt für ganzrationale Funktionen:
- f(x) = 3x^4+2x³-4x²+x-16 ist nicht achsensymmetrisch zur y-Achse.
- f(x) = 3x^4+4x²-16 ist achsensymmetrisch zur y-Achse.
- Für ganzrationale Funktionen gibt es eine einfache Regel:
- Kommt x nur mit geradzahligen Exponenten vor, dann ist der Graph achsensymmetrisch zur y-_Achse.
- Dabei gilt: x ist wie x¹ und damit nicht geradzahlig. Aber 4 ist wie 4·x° und damit geradzahlig.
- Eine reine Zahl gilt als geradzahlige Potenz von x.
- Mehr unter Exponentenregel der Graphensymmetrie ↗
