Basiswissen

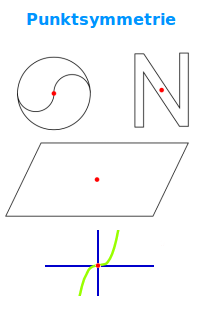
Von Punktsymmetrie spricht man, wenn eine Figur (Geometrie, Graph) an einem Punkt gespiegelt werden kann und die Figur nach der Spiegelung wieder genauso aussieht wie vor der Spiegelung. In der Fachsprache heißt das, dass die Figur auf sich selbst abgebildet wird.

Bildbeschreibung und Urheberrecht — Etwas wird um einen Punkt gedreht und ist danach nicht vom ursprünglichen Objekt zu unterscheiden. Wenn das funktioniert, dann spricht man von Punktsymmetrie.☛

Definition von Punktsymmetrie

Eine Figur ist punktsymmetrisch, wenn man sie an einem Punkt spiegeln kann und sie dadurch auf sich selbst abgebildet wird. Das ist identisch mit der Definition, dass es einen Punkt gibt, um den man die Figur um 180° drehen kann und das so entstehende Bild genauso aussieht wie das Bild vor der Drehung. Man sagt, die Figur wird auf sich selbst abgebildet.^[1]

Geometrie

Hier meint es, dass eine Figur ein Symmetriezentrum hat.

Man kann zum Beispiel ein Quadrat um seine Mitte drehen.

Eine 90°-, 180°-, 270°- oder 360°-Drehung würde man nicht erkennen.

Lies mehr dazu unter Punktsymmetrie in der Geometrie ↗

Funktionenlehre

Ein Graph wird um 180° um den Ursprung (0|0) gedreht.

Oder der Graph wird um einen anderen Punkt gedreht.

Mehr unter Punktsymmetrie von Graphen ↗

Synonyme

Zentralsymmetrie ↗

Punktsymmetrie ↗

Fußnoten

[1] Die Definition der Punktsymmetrie stammt aus: Guido Walz: Spektrum Lexikon der Mathematik. Band 5: Sed bis Zyl; 2002; ISBN: 3-8274-9437-1