Punktspiegelung von Graphen
Anleitung
© 2016
- 2026
Basiswissen
Graphen können an beliebigen Punkten im Koordinatensystem punktgespiegelt werden. Hier wird aber nur die Punktspiegelung im engeren Sinn behandelt: eine Spiegelung am Koordinatenursprung (0|0).
Anleitung
- Beispiel:
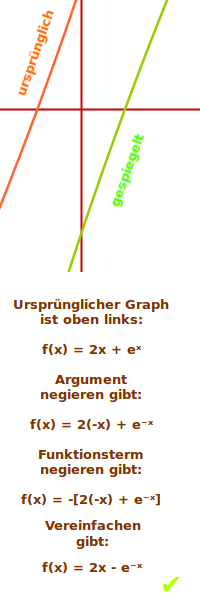
- f(x)=2x+e^x
- Ein gegebener Graph mit Funktionsgleichung soll punktgespiegelt werden.
- Dazu negiert man zuerst überall das Funktionsargument.
- Anschließend negiert man den gesamten Funktionsterm.
- Negieren heißt: das Vorzeichen wechseln (+ wird - und - wird +).
- Der Funktionsargument ist das was eingesetzt wird, meistens das x.
- Beispiel: Der Graph von f(x)=2x+e^x soll am Punkt (0|0) gespiegelt werden.
- Funktionsargument negieren gibt: f(x)=2(-x)+e^(-x)
- Funktionsterm negieren gibt: f(x)=-[(2(-x)+e^(-x)]
- Vereinfachen ergibt:
- f(x)=2x-e^(-x)