Steigung
Übersicht
© 2016
- 2025
Basiswissen|
Arten|
Geradensteigung|
Sekantensteigung|
Tangentensteigung|
f'(x)|
Steigung bestimmen|
Schreibweisen|
Umwandlungen|
Sachwelt
Basiswissen
Steigung an sich sagt, wie steil etwas nach oben oder unten geht. In der Mathematik berechnet man die Steigung meist über ein Steigungsdreieck. Die Steigung ergibt sich dann aus der Höhe dieses Dreiecks geteilt durch seine Breite.
Arten
Geradensteigung
Die Steigung einer Geraden ist die Grundlage für alle weiteren Aspekte der Steigung in der Mathematik. Einige wenige Grundfakten geben einen ersten Einstieg:
- Geht die Gerade von links nach rechts bergauf, ist die Steigung positiv.
- Geht die Gerade von links nach rechts bergab, ist die Steigung negative.
- Verläuft die Gerade von links nach rechts waagrecht, ist die Steigung 0.
- Geht die Gerade steil bergauf, ist die Steigung eine große Zahl (z. B. 9).
- Geht die Gerade steil bergab, ist die Steigung eine kleine Zahl (z. B. -9).
In der Normalform der Geradengleichung, oft geschrieben als y=mx+b ist der Faktor vor dem x, hier also das m, der Platzhalter für die Zahl der Steigung. Siehe auch 👉 y=mx+b
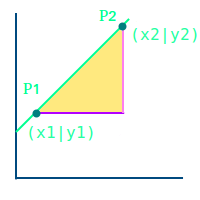
Um die Steigung einer Geraden zu berechnen, kann man zwei beliebige Punkte, P1 und P2, auf einer Geraden eintragen. Die Steigung ist dann gleich dem Quotienten (geteilt) der Differenz (minus) der Y-Werte und der Differenz der X-Werte. Für P1(1|2) und P2(4|8) erhält man dann 8-2 geteilt durch 4-1, also 6 geteilt 3, also 2 für die Steigung. Siehe mehr unter 👉 Geradensteigung berechnen
Die anschauliche Grundlage dieses Verfahrens zur Berechnung der Steigung einer Geraden ist das Steigungsdreieck. Das Steigungsdreieck für zwei Punkte einer Geraden kann man immer so zeichnen: verbinde die zwei Punkt mit einer geraden Strecke, zeichne eine waagrechte Strecke durch P1. Diese waagrechte (links-rechts) Strecke muss so lang sein, dass sie auch ober- oder unterhalb von P2 entlang geht. Zeichne dann eine senkrechte Strecke (oben-unten) durch P2. Diese senkrechte Strecke muss so lang sein, dass sie auch links oder rechts von P1 entlang geht. Man sieht dann, wie aus diesen drei Strecken ein Dreieck entstanden ist. Dann teilt man die Höhe dieses Dreiecks durch seine Breite. Das Ergebnis ist die Steigung m. Siehe dazu auch den ausführlichen Artikel 👉 Steigung aus Steigungsdreieck
Sekantensteigung
Als Sekante bezeichnet man eine Gerade, die durch zwei vorher festgelegte Punkt einer Kurve geht (ein Kurve in der Mathematik kann auch eine Gerade sein). Die Sekantensteigung wird genauso berechnet wie die Steigung einer Geraen über ein Steigungsdreieck. Siehe mehr im Artikel 👉 Sekantensteigung
Tangentensteigung
Eine Tangente an einem Punkt einer Kurve ist eine Gerade, die a) durch genau diesen Punkt hindurch geht und b) dort auch dieselbe Steigung hat wie die Kurve. Die Tangentensteigung ist identisch mit dem Wert der ersten Ableitung f'(x) an diesem Punkt. Siehe mehr unter 👉 Tangentensteigung
f'(x)
f'(x) liest man als "f Strich von x". Dieser Ausdruck steht für die sogenannte erste Ableitung einer Funktion. Zum Beispiel hat die Funktion f(x)=x² die erste Ableitung f'(x)=2x. Um die Steigung an der Stelle (Stelle = x-Wert) x=4 zu berechnen setzt man die Zahl 4 für x in die erste Ableitung ein: f'(4)=8. Damit gibt die Zahl 8 die Steigung von f(x) an der Stelle 4. Siehe mehr unter 👉 erste Ableitung
Steigung bestimmen
Die Idee der Steigung ist einer der wichtigsten Konzepte in der Höheren Mathematik zum Thema Funktionen. Es gibt eine große Anzahl verschiedener Verfahren zur Bestimmung der Steigung:
Die Grundidee zu allen diesen Methoden ist die Steigung aus zwei Punkten. Siehe mehr zu diesen verschiedenen Verfahren im Artikel 👉 Steigung bestimmen
Schreibweisen
Die Steigung steht eigentlich nur für die Idee der Steilheit. Wie steil etwas ist, etwa ein Wanderweg im Wald oder eine Kurve in einem Graphen, kann man auf sehr viele verschiedene Weisen angeben.