Tangentensteigung
Definition
© 2016
- 2025
Basiswissen
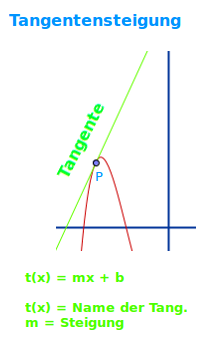
Die Tangente im Sinne der Analysis (Funktionsgraphen) ist immer eine Gerade. Sie schneidet oder berührt den Graphen an einem Punkt so, dass sie dort dieseelbe Steigung hat wie der Graph. Die Tangentensteigung ist dann auch die Steigung des Graphen an diesem Punkt.
Eigenschaften der Tangente
- Die Tangente ist immer eine Gerade.
- Geschrieben wird sie oft als t(x) = mx+b.
- Eine Tangente gehört immer zu einem einzigen Punkt P eines Graphen f(x).
- Dieser Punkt darf aber kein Knickpunkt und keine Lücke im Graphen sein.
- Die Tangente ist dann die Gerade, die genau gleich der Steigung ...
- des Graphen f(x) an diesem Punkt P ist.
- Mehr unter 👉 Kurventangente
Tangentensteigung
- Die Steigung m der Tangente t(x) gehört immer zu einem Punkt von f(x).
- Man berechnet erst die Steigung von f(x) für diesen Punkt.
- Das macht man meistens über die erste Ableitung f'(x).
- Diese Steigung ist dann auch gleich der Tangentensteigung.
- Siehe auch 👉 Tangentensteigung berechnen
Tangentengleichung
- Kennt man von einer Tangente einen Punkt P und die Steigung m, ...
- kann man daraus immer die Gleichung t(x) für aufstellen.
- Siehe unter 👉 Tangentengleichung aufstellen