Tangente
Definitionen
Basiswissen
In der Geometrie und für Funktionsgraphen: das Wort Tangente hat zwei ähnliche aber dennoch leicht unterschiedliche Bedeutungen, etwa für einen Kreis oder für den Graphen einer Funktion. Das ist hier kurz vorgestellt.
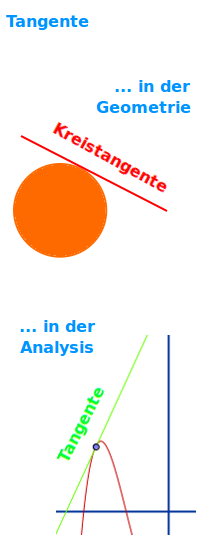
Tangente in der Geometrie
- In der Geometrie ist die Tangente immer eine Gerade ...
- die etwas anderes in einem Punkt nur berührt[1].
- Berühren meint: nicht schneiden oder eindringen.
- Siehe als Beispiel die Kreistangente ↗
Tangente in der Analysis
- Analysis meint: die Mathematik von Ableitungen und Steigungen.
- Man hat immer irgendeine Funktion f(x) mit Graph gegeben.
- Eine Tangente gehört immer zu einem Punkt auf dem Graphen:
- Die Tangente im Punkt P einer Funktion f(x) ist diejenige ...
- Gerade, die durch den Punkt P der Funktion f geht und ...
- im Punkt P diesselbe Steigung hat wie f(x).
- Siehe auch Kurventangente ↗
Definitionen zu Tangenten
Rechnungen
Das Wort Tangente als Mehrdeutigkeit
Das Wort Tangente wird innerhalb der Mathematik also mit mindestens zwei unterschiedlichen Bedeutungen verwendet. Einmal darf sie nur genau einen Punkt mit einer anderen Figur gemeinsam haben (Kreis), ein anderes Mal dürfen es beliebig viele sein (Funktionsgraphen). Wenn diese Doppeldeutigkeit nicht klar gemacht wird, ist das Wort Tangente ein Beispiel für eine schädliche Mehrdeutigkeit ↗
Synonyme von Tangente
Fußnoten
- [1] Bronstein, Semendjawew, Musiol, Mühlig: Taschenbuch der Mathematik. 10. Auflage (2016). Edition Harri Deutsch. Verlag Europa-Lehrmittel. ISBN: 978-3-8085-5789-1. Seite 251 ff. Siehe auch Der Bronstein ↗
- [2] Guido Walz: Spektrum Lexikon der Mathematik. Band 5: Sed bis Zyl; 2002; ISBN: 3-8274-9437-1. Siehe auch Spektrum Lexikon der Mathematik ↗
- [3] 1857, Tangente mit Berührpunkt: "Tangente, in der Geometrie eine gerade Linie, welche eine krumme Linie in der Art berührt, daß sie mit dieser nur einen Punkt gemein hat und in diesem mit der Curve gleiche Richtung. Beim Kreise erhält man eine T. durch Errichtung einer Senkrechten im Endpunkte eines Halbmessers. In der Trigonometrie heißt T. eines Kreisbogens eine Gerade, welche senkrecht auf einen Radius in dessen Endpunkt errichtet und an dem einen Ende von diesem Radius, am andern Ende von der durch den andern Endpunkt des Bogens gezogenen [409] Secante begränzt ist. Dieser trigonometrischen T.n, die somit eine bestimmte Länge haben, was bei den geometrischen nicht der Fall ist, bedient man sich sowie der Sinus, Cosinus etc. zur Auflösung der Dreiecke. Sie sind mit Beziehung auf einen bestimmten Halbmesser für jeden Kreisbogen berechnet u. ihre Werthe od. deren Logarithmen in trigonometrischen Tafeln verzeichnet. – Bei den Klavierinstrumenten heißt T. derjenige Theil auf den Tasten, welcher beim Anschlagen der Taste die Saiten berührt und zum Tönen bringt." In: Herders Conversations-Lexikon. Freiburg im Breisgau 1857, Band 5, S. 409-410. Online: http://www.zeno.org/nid/20003536637
- [4] 1863, Tangente schneidet nicht wirklich: "Tangente (v. lat.). 1) so v.w. Berührende, d.h. eine Gerade, welche mit einer krummen Linie einen Punkt gemein hat u. beiderseits wenigstens bis zu endlicher Entfernung verlängert ganz auf Einer Seite der Curve liegt. Man kann sie als eine Schneidende betrachten, deren beide Schneidungspunkte in einen zusammenfallen. Für parallele Coordinaten ist, wenn y = fx die Gleichung der Curve ist, die Gleichung der T. im Punkte x, y, folgende: y – y, = dy,/dx,(x – x). Ist die Gleichung der Curve vom zweiten Grade, wie beim Kreise u. den Kegelschnitten, so hat die T. mit der Curve nur den Berührungspunkt gemein. Ist jene höheren Grades od. transscendent, so kann die T. die Curve noch in anderen Punkten berühren u. schneiden; 2) trigonometrische T. eines spitzen Winkels im achtwinkeligen Dreieck, der Quotient der gegenüberliegenden Kathete dividirt durch die anliegende, s. Trigonometrie; 3) so v. w. Daumen 4); 4) bei einer Spieluhr Haken od. Hebel, welche zunächst von den Stiften der Walze ergriffen werden u. das Erklingen des bestimmten Tones bewirken; 5) der metallene Stift od. das kleine Stück Blech, welches beim Clavier an die Saiten schlägt u. diese tönen macht; auch wohl 6) der ganze im Inneren des Claviers befindliche Theil des Clavis, s.d. 2); 7) (Hdlgsw.), so v.w. Antheil." In: Pierer's Universal-Lexikon, Band 17. Altenburg 1863, S. 229. Online: http://www.zeno.org/nid/20011065443
- [5] 1909, vor allem im Sinn der Analysis: "Tangente (lat., »Berührende« oder Berührungslinie) einer krummen Linie oder Kurve (s. d.) heißt jede Gerade, welche die Kurve in einem Punkte so schneidet, daß in diesem Punkte zwei Schnittpunkte der Geraden und der Kurve zusammenfallen. Man sagt dann, daß die T. die Kurve in diesem Punkte (dem Berührungspunkte) berührt. [Hier befindet sich im Originaltext eine Tabelle] Die T., die eine gegebene Kurve (s. Figur) in einem gegebenen Punkte A berührt, findet man, indem man durch A eine Gerade AB nach einem andern Punkte B der Kurve zieht und dann B auf der Kurve nach A hin wandern läßt. Je näher B dem A kommt (in der Figur sind vier aufeinanderfolgende Lagen B, B1, B2, B3 von B angegeben), um so näher kommt die Gerade AB einer gewissen Grenzlage AC, die sie schließlich erreicht, wenn B mit A zusammenfällt. Bezieht man eine ebene Kurve auf zwei zueinander senkrechte Koordinatenachsen (s. Koordinaten), so nennt man Subtangente des Punktes A das Stück der Abszissenachse, das von der zu A gehörigen T. und von der durch A gezogenen Parallelen zur Ordinatenachse begrenzt wird. T. einer krummen Fläche in dem Punkte A heißt jede Gerade, welche die Fläche in A so schneidet, daß in A zwei Schnittpunkte der Geraden und der Fläche zusammenfallen, oder, was dasselbe ist, jede Gerade, die eine auf der Fläche liegende und durch A gehende Kurve in dem Punkt A berührt. Die zu einem Punkt A der Fläche gehörigen Tangenten liegen alle in einer Ebene, von der man sagt, daß sie die Fläche in A berührt, und die man die zu A gehörige Tangentialebene der Fläche nennt. Beim Kreise steht die T. stets senkrecht auf dem Halbmesser, der nach dem Berührungspunkt geht; dasselbe gilt bei der Kugel von der Tangentialebene. – In der Trigonometrie bezeichnet man als T. eines Winkels den Bruch, dessen Zähler der Sinus und dessen Nenner der Kosinus des Winkels ist. – Beim alten Klavichord hießen Tangenten die auf den hintern Tastenenden stehenden Metallzungen, welche die Saiten nicht anriffen, wie die Federposen des Kielflügels, sondern nur streiften (tangierten), daher auf eine ähnliche Weise tonerzeugend wirkten wie der Bogen der Streichinstrumente (s. Klavier, S. 101)." In: Meyers Großes Konversations-Lexikon, Band 19. Leipzig 1909, S. 306-307. Online: http://www.zeno.org/nid/20007561059
- [6] 1911, Berührungpunkt, auch als Tangens: "Tangénte (lat., »Berührende«), jede gerade, nur in einem Punkt mit einer Kurve zusammenfallende Linie; Tangentialebene das entsprechende bei Flächen. Die T. eines Kreises steht senkrecht auf dem Radius des berührten Kreispunkts. Die T. eines Winkels (tan, tang, tg) im rechtwinkligen Dreieck ist das Verhältnis der dem Winkel gegenüber liegenden Seite zur anliegenden." In: Brockhaus' Kleines Konversations-Lexikon, fünfte Auflage, Band 2. Leipzig 1911., S. 806. Online: http://www.zeno.org/nid/20001606530
