Kreis
◯ Definition und Übersicht
Basiswissen
Ein Kreis ist ist die Menge aller Punkte, die gleich weit von ihrem gemeinsamen Mittelpunkt entfernt sind. Der Kreis spielt in der Geometrie eine große Rolle. Hier sind die wichtigsten Fachworte und Formeln zusammengestellt.
Zwei Bedeutungen von Kreis
- Das Wort Kreis hat zwei unterschiedliche aber eng verwandte Bedeutungen.
- Es meint zum einen nur die die Linie am Rand, genauer die Kreislinie ↗
- Es kann aber auch die ganze Fläche meinen, genauer die Kreisfläche ↗
Der Kreis in der Mathematik (Berechnungen)
In der Mathematik wird der Kreis meist mit der Kreislinie (Rand) gleichgesetzt. Man definiert dann: Ein Kreis ist die Menge alle Punkte, die denselben Abstand zu einem gemeinsamen Mittelpunkt haben und die alle in der selben Ebene liegen. Lässt man die Bedingung wegfallen, dass die Punkte alle in einer Ebene liegen müssen, erhält man dadurch die Definition für eine Kugel. Berechnungen rund um einen Kreis sind zusammgengestellt auf der Seite zu Kreisformeln ↗
Der Kreis in der Philosophie
Seit der griechischen Antike gibt es die Idee, dass es ideale oder perfekte Formen und Körper gibt. Die sogenannten platonischen Körper sind dafür ein Beispiel. Zu den "vollkommenen Dingen" gehört Aristoteles (384 bis 325 v. Chr.) zufolge auch der Kreis. Als Begründung führte er an, dass nur der Kreis, anders als etwa eine Gerade, keinen Anfang und kein Ende habe[1]. Aus der Idee des idealen Kreises folgte dann über mehrere Zwischenschritte ein gesamtes Weltbild. Seit Aristoteles gingen Astronomen davon aus, dass Kreise und Kugeln die Grundbausteine der Himmelserscheinen (Sterne, Planeten, Mond, Sonne) sind. Dieses Bild zu überwinden sollte dann fast 2000 Jahre dauern. Die Idee kreisförmig oder kugelig aufgebauter Bewegungen am Himmel führte zunächst zur Idee von Himmelssphären (externer Link)
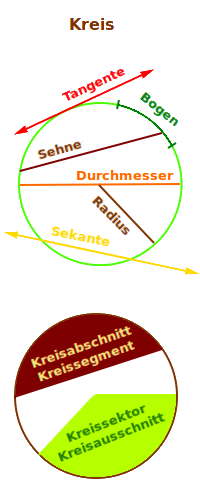
Fachworte
Konstruktionen
Flächenformeln
Berechnungen
Kuriositäten
Kreise
- Stonehenge, Hexenringe oder der Äquator:
- Solche und weitere Beispiele unter Kreise ↗
Fußnoten
- [1] "das Vollkommene geht von Natur aus dem Unvollkommenen voraus, und der Kreis gehört zu den vollkommenen Dingen, anders als irgend eine gerade Linie: weder die unendliche (Gerade) diese hätte dann nämlich Grenze und Ende noch eine unter denen, die begrenzt sind denn bei allen (diesen) gibt es etwas, was außerhalb (ihrer) liegt, da es möglich ist, jede beliebige von ihnen zu verlängern." In: Aristoteles Werke in deutscher Übersetzung. Begründet von Ernst Grumach. Herausgegeben von Hellmut Flashar. Band 12. I. Teil III Über den Himmel. Übersetzt und Erläutert von Alberto Jori. Akademie Verlag. Berlin. 2009. ISBN: 978-3-05-004303-6. Dort der Absatz a 20 auf Seite 23. Siehe auch Weltharmonie ↗
