Basiswissen

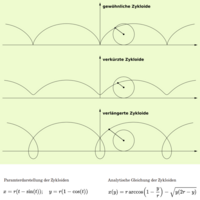
Als Zykloide bezeichnet man die Linie, die entsteht, wenn man einen Stift an einen festen Punkt am Rand eines Kreises hält und den Kreis dann entlang einer geraden Linie auf einem Blatt Papier abrollt. Eng verwandt mit einer Zykloide ist der astronomisch interessante Epizykel ↗

Fußnoten

[1] 1905, Definition: "Zykloïde (griech., »Radlinie«), die ebene Kurve, die ein Punkt auf dem Umfang eines Kreises beschreibt, wenn dieser auf einer geraden Linie, der Grundlinie oder Basis, hinrollt, ohne zu gleiten." Sowie: " Außer der bisher betrachteten sogen. gemeinen Z. unterscheidet man noch Epizykloiden und Hypozykloiden; sie werden von einem Punkte des Kreisumfanges beschrieben, wenn der Kreis statt auf einer Geraden auf einem festen Kreise hinrollt, und zwar die eine oder die andre, je nachdem der bewegliche Kreis auf der äußern oder auf der innern Seite des festen Kreises hinrollt." In: Meyers Großes Konversations-Lexikon, Band 20. Leipzig 1909, S. 1051-1052. Online: http://www.zeno.org/nid/20007735391

[2] 1911, Definition: "Zykloīde (grch.), Radlinie, krumme Linie [c in Abb. 1999], welche ein Punkt a einer Kreislinie k beschreibt, die auf einer geraden Linie g rollt; diese Z. heißt gemeine Z. Rollt der Kreis auf der äußern oder innern Seite der Peripherie eines zweiten Kreises [K in Abb. 1999], so heißt die Kurve im ersten Fall Epi-Z. (e), im letztern Hypo-Z. (h). Die Z. besitzt die Eigenschaft der Tautochrone (s.d.)." In: Brockhaus' Kleines Konversations-Lexikon, fünfte Auflage, Band 2. Leipzig 1911., S. 1042. Online: http://www.zeno.org/nid/2000170480X

zur Bildbeschreibung mit Autoren- und Urheberinfos — Die Bilder zeigen, wie verschiedene Formen einer Zykloiden durch ein Abrollen eines Kreises entlang einer geraden Linie entstehen. Kmhkmh