Nullstellen von kubischen Funktionen bestimmen
Methoden
© 2016
- 2025
Basiswissen|
Was ist eine Nullstelle?|
Kurzbeispiel|
Was heißt kubisch?|
Wie viele NS gibt es?|
Graphisch bestimmen|
Rechnerische Methoden|
Rechnerisch: Umformen|
Rechnerisch: Probieren|
Rechnerisch: Teilermethode|
Rechnerisch: Faktorisieren|
Ablesen|
Polynomdivision|
Horner-Schema|
Sonstiges
Basiswissen
Nullstellen von kubischen Funktionen, auch ganzrationale Funktionen dritten Grades genannt, sind teilweise sehr aufwändig zu berechnen. Es gibt einige eher leicht lösbare Sonderfälle aber auch einige nur sehr schwer lösbaren Typen von Gleichungen. Die Wahl der richtigen Methode kann viel Mühe sparen. Hier stehen die wichtigsten Methoden in einer kurzen Übersicht.
Was ist eine Nullstelle?
Das ist der x-Wert, bei dem der Graph einer Funktion die x-Achse schneidet. Dort hat den Graph den y-Wert Null, daher der Name. Die Nullstelle ist also eine Zahl auf der x-Achse. Setzt man diesen x-Wert in die Funktion f(x) ein, dann kommt für y immer die Zahl 0 heraus. Mehr zur Definition steht im Artikel 👉 Nullstelle
Kurzbeispiel
Z. B. von f(x) = x·(x²-4): Nullstellen sind die x-Werte bei denen der y-Wert zu 0 wird. Bei der Funktion f(x)=x·(x²-4) wären das die x-Werte 0, -2 und 2, denn: f(0)=0, f(-2)=0 und f(2)=0.
Was heißt kubisch?
- f(x) = ax³ + bx² + cx +
- Jede Funktion, die man in die obige Form umformen kann, heißt kubisch.
- Kubische Funktionen heißen gauch ganzrationale Funktionen dritten Grades.
- Beispiele: f(x) = x³-9x²+26x-24 oder f(x) = 4x³+4x²
- Mehr unter 👉 Kubische Funktion
Wie viele NS gibt es?
Eine kubische Funktion hat mindestens eine Nullstelle. Sie hat höchstens drei Nullstellen. Sie kann auch genau zwei haben. Siehe auch den allgemeinen Artikel zur 👉 Anzahl von Nullstellen
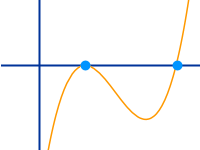
Graphisch bestimmen
- Man kann sich den Graphen der Funktion ausgegeben lassen.
- Ideal dazu ist ein graphischer Taschenrechner oder ein Computerprogramm.
- Dort, wo der Graph die x-Achse schneidet, liegen die Nullstellen.
- Die x-Werte dieser Schnittpunkte sind die gesuchten Nullstellen.
- Mehr unter 👉 Nullstellen aus Graph
Rechnerische Methoden
Es gibt viele verschiedene Verfahren. Bei allen Verfahren setzt man f(x) erst einmal gleich 0. Ab dann ist die Lösungsweise dieselbe wie die beim Lösen einer kubischen Gleichung. Es gibt mehrere Rechenmethoden:
Rechnerisch: Umformen
f(x) = 2x³-128: man setzt gleich 0 und stellt dann den Funktionsterm um nach x. Das gibt hier im Beispiel x=∛64 oder x=4. Lies mehr unter 👉 reinkubische gleichungen lösen
Rechnerisch: Probieren
f(x) = x³-8: der Funktionsterm ist sehr einfach: Für x einfache Zahlen wie 0, 1, 2 einsetzen. Wenn f(x) Null wird, hat man eine Nullstelle gefunden. Mehr unter 👉 kubische Gleichungen über Probieren
Rechnerisch: Teilermethode
f(x) = 1x³-6x²+11x-6: es gibt nur ganzzahlige Koeffizienten. In diesem Fall gibt es nur sehr wenige mögliche Lösungen, die man schnell durch Einsetzen überprüfen kann. Mehr dazu unter 👉 Kubische Gleichungen über Teilermethode
Rechnerisch: Faktorisieren
f(x) = 3x³ - 2x² + 1x: der Funktionsterm hat nur Glieder mit x: Ein x aus dem Funktionsterm ausklammern. Wenn das geht, hat man eine Nullstelle bei x=0. Der restliche Klammerterm ist dann eine quadratische Gleichung. Sie kann man mit der normalen pq-Formeln lösen. Mehr unter 👉 Kubische Gleichungen über Faktorisieren
Ablesen
f(x) = (x-1)·(x-2)·(x+4): die Funktionsgleichung liegt schon in faktorisierter Form als eine Malkette vor. Dann gilt der Satz vom Nullprodukt und man kann die NS direkt ablesen, mehr unter 👉 Nullstellen von kubischen Funktionen über Ablesen
Polynomdivision
f(x) = 19x⁵ + 20x⁴ + 2x: Der Funktionsterm ist schwierig, aber eine Lösung ist schon bekannt: Kann man kein x ausklammern und hat man eine Lösung der Gleichung irgendwoher anders, dann teilt man per Polynomdivision den Funktionsterm durch den Klammerterm (x-Lösung). Geht die Polynomdivision glatt auf, dann ist das Ergebnis eine quadratische Gleichung, die man wieder mit der pq-Formeln lösen kann. Siehe auch den Artikel zur 👉 Polynomdivision
Horner-Schema
Ist ähnlich wie die Polynomdivision. Auch hier muss man wieder eine erste Nullstelle kennen, um überhaupt anfangen zu können. Das Verfahren ist hier nicht erklärt.
Sonstiges
Zwei andere Lösungswege sind die Cardanische Formel sowie das Newton-Verfahren. Dieses ist recht zeitaufwändig zu rechnen, jene recht schwer zu verstehen. Beide Wege kommen normalerweise, wenn überhaupt, erst in einem Studium vor.