Weder noch
In der Aussagenlogik steht die sogenannte Peircesche Relation NOR dafür, dass von zwei Aussagen keine wahr ist. NOR ist die Abkürzung für NOT OR, also „Weder noch“, als Zeichen => ⊽
Chemie
Bor - chemisches Zeichen B, Ordnungszahl 5 - ist ein in einer tetragonalen und zwei rhombischen Modifikationen vorkommendes, in kistalliner Form grauschwarzes, sehr hartes und reaktionsträges, nichtmetallisches chemisches Element. Siehe auch => Bor Datenblatt
Als griechische Silbe: geben, Geschenk, Gabe
Eine Silbe dot oder dor steht oft für die Idee, dass etwas gegeben wird. Ein Antidot ist ein Gegengift, das man gibt. Eine Dotation ist eine (Geld)Gabe, ähnlich einem Geschenk. => Ganzen Artikel lesen …
… als griechische Silbe: heben, aufheben, schweben, z. B. in => Meteor
 XNOR
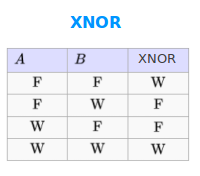
XNOR
Logik
XNOR heißt: die Aussagen sind entweder alle wahr oder sie sind alle falsch. Dazu steht hier die Wahrheitstafel. => Ganzen Artikel lesen …
Französisch für schwarz beim Roulette-Spiel
… Häufig gebrauchte Abkürzung für eine => Nebenrechnung
… z. b. eine kubische Parabel, siehe unter => keine normale Parabel
… etwa die 0,5-te Wurzel, siehe unter => r-te Wurzel
 Abnormal
Abnormal
Wertend
„Der Mann hat einen abnormal hohen Ruhepuls von über 80 Schlägen pro Minute“. Wer so etwas sagt, deutet meist auch eine Ablehnung oder einen Vorwurf mit an, etwa: „Er sitzt den ganzen Tag nur herum, trinkt süße Cola und isst fette und süße Sachen. Das finde ich nicht gut.“ Nicht normal aber wertfrei meint hingegen das Wort => unnormal
… z. b. eine kubische Parabel, siehe unter => keine normale Parabel
… alle außer den Quadratwurzeln, mehr unter => Wurzelarten
… etwa die 0,5-te Wurzel, siehe unter => r-te Wurzel
Zahlen die zu keiner Basis normal sind
Als normal bezeichnet man - einfach gesprochen - Zahlen, bei denen alle Ziffern in den Nachkommastellen gleich häufig und vollkommen unregelmäßig vorkommen. Rationale Zahlen können nie normal sein. Rationale sind Zahlen, die sich als Bruch darstellen lassen. Ihre Nachkommastellen sind früher oder später immer periodisch. Daher gibt es in den Nachkommastellen eine Regelmäßigkeit. Somit muss eine normale Zahl immer irrational sein. => Ganzen Artikel lesen …
Anleitung
In einem xyz-Koordinatensystem sind ein Punkt (A|B|C) sowie eine Ebene in der hesseschen Normalenform x·n₀ = d gegeben. Eine einfache Formel berechnet den Abstand zwischen Punkt und Ebene. => Ganzen Artikel lesen …
Vektorrechnung
Achsenabschnittsform in Allgemeine Normalenform: hier wird kurz die Grundidee vorgestellt, wie man eine gegebene Form oder Darstellungsweise einer Ebene in eine gesuchte andere Form der Ebene umwandelt. => Ganzen Artikel lesen …
Vektorrechnung
Achsenabschnittsform in Hessesche Normalenform: hier wird kurz die Grundidee vorgestellt, wie man eine gegebene Form oder Darstellungsweise einer Ebene in eine gesuchte andere Form der Ebene umwandelt. => Ganzen Artikel lesen …
Vektorrechnung
x/8+y/8+z/4=1 ist eine typische Gleichung für eine Ebene in Achsenabschnittsform. Dieselbe Ebene geschrieben in Punkt-Normalenform (X-p)·n=0 ist mit Zahlen ausgeschrieben (X-(4|4|0))·(1|1|2)=0. Hier ist die Umwandlung kurz vorgestellt. => Ganzen Artikel lesen …
Mathematiker
Whitehead lebte von 1861 bis 1947. Geboren wurde er im englischen Ramsgate, er starb in Massachusetts, in den USA. Berühmt wurde er mit seinem Werk „Principia Mathematica“, das er gemeinsam mit seinem Schüler Bertrand Russel verfasste. Darin versuchten die beiden, die Mathematik ganz in der Logik zu gründen. Whitehead kritisierte auch das damalage englische Bildungssystem. 1924 ging er als Professor in die USA, wo er sich seinen philosophisch-metaphysischen Interessen widmete. Siehe auch => Alfred North Whitehead (Zitate)
Zitate von Whitehead rund um Wissenschaft
- => Whiteheadsche Kohärenz
… Rechenbeispiel unter => Normalform in Allgemeine Form
… Rechenbeispiel unter => Allgemeine Form in Normalform
Allgemeine Form AF in Normalform NF umwandeln
Hier geht es um die Umwandlung von Funktionsgleichungen mit f(x). Funktionsgleichungen sollte man nicht mit Äquivalenzumformen verändern. Man darf immer nur den Funktionsterm selbst mit Termumformungen ändern. => Ganzen Artikel lesen …
Wie man die Normalform herstellt
Mit der pq-Formel kann man jede quadratische Gleichung lösen. Dazu muss die Gleichung aber in der sogenannten Normalform vorliegen. Tut sie das nicht, muss man sie erst umwandeln. Das x² meint x-quadrat: => Ganzen Artikel lesen …
… Rechenbeispiel unter => Allgemeine Form in Normalform
Vektorrechnung
n·x = d ist die allgemeine Normalenform der Ebene. Ausgesprochen heißt das: n skalar multipliziert mit x ergibt für eine gegebene Ebene immer denselben Zahlenwert d. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Vektorrechnung
X·[1|1|2]=8 ist eine typische Ebenengleichung in der sogenannten allgemeinen Normalenform. Sie kann ohne großen Rechenaufwand leicht umgewandelt werden in die sogenannte Achsenabschnittsform x/8+y/8+z/4=1. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
Vektorrechnung
Eine Ebenengleichung in allgemeiner Normalenform ist zum Beispiel x·(3|4|0)=20. Dieselbe Ebene dargestellt in der Hesseschen Normalenform ist x·(3/5|4/5|0)=4. Die Umwandlung ist hier kurz erklärt. => Ganzen Artikel lesen …
Vektorrechnung
X·[1|1|2]=8 ist eine typische Gleichung für eine Ebene in der allgemeinen Normalenform. Der allgemeine Bauplan ist X·n=d mit X als einen beliebigen Ortsvektor, n als einem sogenannten Normalenvektor und d als einer reinen Zahl. In Koordinatenform ist dieselbe Ebene bestimmt über die Gleichung 1x+1y+2z=8. Die Umwandlung erfordert keinerlei Rechnung. Sie ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Vektorrechnung
Eine Ebene in der allgemeinen Normalenform X·n=d kann immer in die Parameterform x = p + r·v1 + s·v2 mit p als Stützvektor und den Richtungs- oder Spannvektoren v1 und v2 umgewandelt werden. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Vektorrechnung
x·[1|1|2]=8 ist eine Beispiel für eine Ebenengleichung in der allgemeinen Normalenform. Dieselbe Ebene geschrieben als (x-(4|4|0))·(1|1|2)=0 ist die sogenannte Punkt-Normalenform der Ebene. Dabei steht das x hier in beiden Fällen für einen Vektor und nicht für eine Zahl. Beide Formen werden oft salopp auch kurz nur als die Normalenform bezeichnet. Hier wird kurz die Umwandlung vorgestellt. => Ganzen Artikel lesen …
Polarstern
Alpha ursae minor ist lateinisch für den Polarstern Polaris. Das Alpha sagt: es ist der hellste Stern in seinem Sternbild. Das ursae sagt: es geht um das Sternbild „Bär“ (latein für des Bären). Minor sagt: klein, es geht also um das Sternbild "kleiner Bär". Der kleine Bär wird oft auch kleiner Wagen genannt. Lies mehr zu dem Stern unter => Polaris
Mathematik
Eine anormal-komplexe Zahl z ist definiert über z = a+bj mit j²=1. Dazu ein Rechenbeispiel zur Multiplikation: (4+2j)·(5+3j) = 20 + 12j + 10j + 6j² = 26 + 22j. Die anormal-komplexe Zahl ist ein Sonderfall einer hyperkomplexen Zahl. Siehe auch => komplexe Zahl
… nicht normal, eine => Anomalie
… etwa die 0,5-te Wurzel, siehe unter => r-te Wurzel

