Kombinatorik
Einführung
Basiswissen
Wie man große Anzahlen (geschickt) abzählt: die Kombinatorik ist ein Teilgebiet der Mathematik. Ein typische Fragestellung ist: wie viele verschiedene Möglichkeiten gibt es, dass man aus 5 verschiedenen Kugeln 2 Kugeln auswählt? Hier steht eine kurze Einführung mit Fachworten zum Thema.
Die Grundidee: das Urnenmodell
Alle Fälle hier kann man modellartig mit dem Urnenmodell anschaulich denken: in einer Urne sind n unterschiedliche Objekte. Wenn es in der Urne zum Beispiel 4 verschiedenfarbige Bälle gibt, dann ist n gleich 4. Dann zieht man k mal aus der Urne. Wenn man zum Beispiel 2 mal zieht, dann ist k genau zwei. Aus diesem Grundgedanken leiten sich jetzt vier Fälle ab. Siehe auch den Artikel Urnenmodell ↗
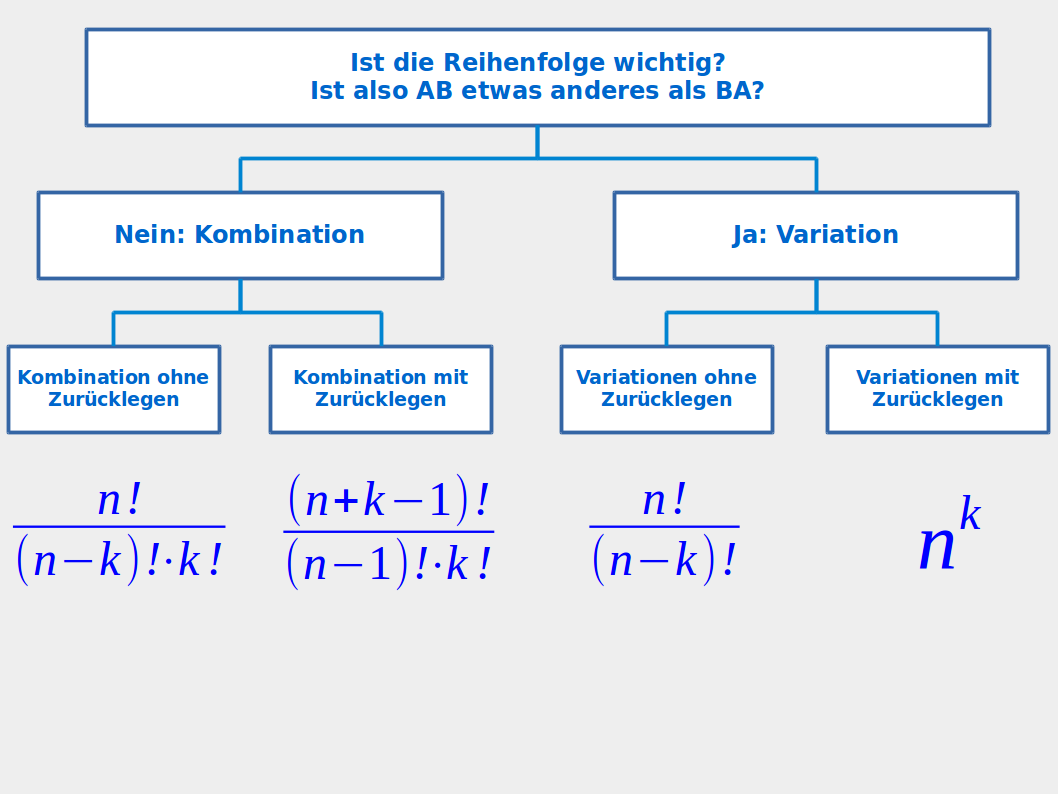
a) Kombinationen ohne Zurücklegen
Aus den Buchstaben A, B und C darf man genau zwei Buchstaben auswählen. Ein bereits ausgewählter Buchstabe darf dabei nicht noch einmal verwendet werden. Die möglichen Kombinationen sind dann AB, AC und BC. Bei Kombinationen - auf Deutsch Zusammenstellungen - ist die Reihenfolge unwichtig. Das heißt, dass zum Beispiel AB und BA dieselbe Kombination sind. Mehr zur Berechnung unter Kombinationen ohne Zurücklegen ↗
b) Kombinationen mit Zurücklegen
Aus den Buchstaben A, B und C darf man genau zwei Buchstaben auswählen. Ein bereits ausgewählter Buchstabe darf dabei auch noch einmal verwendet werden. Die möglichen Kombinationen sind dann AB, AC und BC, AA, BB und CC. Bei Kombinationen - auf Deutsch Zusammenstellungen - ist die Reihenfolge unwichtig. Das heißt, dass zum Beispiel AB und BA dieselbe Kombination sind. Mehr zur Berechnung unter Kombinationen mit Zurücklegen ↗
c) Variationen ohne Zurücklegen
Aus den Buchstaben A, B und C darf man genau zwei Buchstaben auswählen. Ein bereits ausgewählter Buchstabe darf dabei nicht noch einmal verwendet werden. Die möglichen Variationen sind dann AB, BA, AC, CA, BC und CB: Bei Variationen - auf Deutsch Anordnungen - ist die Reihenfolge wichtig. Das heißt, dass zum Beispiel AB und BA zwei verschiedene Variationen sind. Mehr zur Berechnung unter Variationen ohne Zurücklegen ↗
d) Variationen mit Zurücklegen
Aus den Buchstaben A, B und C darf man genau zwei Buchstaben auswählen. Ein bereits ausgewählter Buchstabe darf dabei auch noch einmal verwendet werden. Die möglichen Variationen sind dann AB, BA, AC, CA, BC, CB, AA, BB und CC: Bei Variationen - auf Deutsch Anordnungen - ist die Reihenfolge wichtig. Das heißt, dass zum Beispiel AB und BA zwei verschiedene Variationen sind. Mehr zur Berechnung unter Variationen ohne Zurücklegen ↗
Permutationen
ABC, ACB, BAC, BCA, CAB und CBA sind die sechs möglichen Permuationen der drei Buchstaben A, B und C. Permutationen sind verschiedene, unterscheidbare Anordnungen von einer Anzahl n von unterscheidbaren Elementen. Die Anzahl aller möglichen Permutationen wird berechnet über n! - sprich n Fakultät. Im Beispiel hatten wir drei Buchstaben, also: 3! = 1·2·3 = 6. Möchte man auf eine der vier Modelle von oben zurückgreifen, dann wählt man die Variationen ohne Zurücklegen. Man setzt dann sowohl für n wie auch für k die Zahl 3 ein und erhält darüber das richtige Ergebnis von 6 Möglichkeiten. Mehr unter Permutation ↗
Das Kombinationsproblem der Philosophie
Das sogenannte Kombinationsproblem gehört in die Philosophie des Geistes. Man bezeichnet damit eine Reihe von ungelösten Fragen dazu, wie sich höhere Geist- oder Bewusstseinformen aus elementaren Bausteinen von Geist oder Bewusstsein zusammensetzen sollen. Siehe dazu auch Kombinationsproblem ↗
