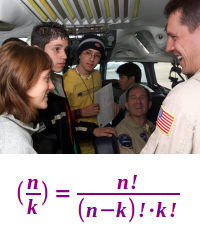Kombinationen ohne Zurücklegen
n über k
© 2016
- 2025
Basiswissen
Zum Beispiel Aeronautik: von 10 Schulfächern muss man genau 4 Wahlpflichtfächer auswählen. Logischerweise kann man ein und dasselbe Fach nicht mehrmals wählen. Es entstehen insgesamt 210 mögliche Kombinationen.
Definition
Eine Kombination ist eine Auswahl von k Elementen aus einer Menge von insgesamt n Elementen. Dabei spielt die Reihenfolge keine Rolle.
Beispiel: Urnenmodell
- Für die drei Buchstaben A, B und C sind folgende Kombinationen möglich, ...
- wenn Wiederholungen nicht erlaubt sind (wie ohne Zurücklegen bei Urne):
- AB (BA wäre das Gleiche)
- AC (CA wäre das Gleiche)
- CB (BC wäre das Gleiche)
Formel
- Kurzversion: n über k
- Langversion: n! durch [n!·(n-k)!]
Legende
- n über k = Binomialkoeffizient 👉 n über k
- ! = Fakultätszeichen, z. B. 3! = 1·2·3 👉 Fakultät
- · = Einfaches 👉 Multiplikationszeichen
Zahlenbeispiel
- Einsetzen:
- 3! geteilt durch (3-2)!2!
- Ausrechnen
- (1·2·3):(1·1·2) = 3
- 3 Kombinationen ist die Lösung.