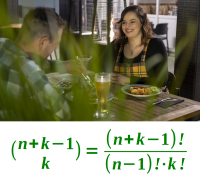Kombinationen mit Zurücklegen
(n + k - 1) über k
© 2016
- 2025
Basiswissen
8 Restaurants bieten für Touristen gemeinsam einen Gutschein an: Man bezahlt einen festen Preis und kann dann an 4 Terminen je ein Restaurant besuchen und all-inclusive Essen. Dabei darf man auch mehrmals dasselbe Restaurant auswählen. Dadurch entstehen 330 mögliche Kombinationen. Das ist hier näher erklärt.
Definition
Eine Kombination ist eine Auswahl von k Elementen aus einer Menge von insgesamt n Elementen. Dabei spielt die Reihenfolge keine Rolle. Die Kombination a-b-b ist also dieselbe Kombination wie b-b-a oder b-a-b. Man unterscheidet weiter zwei Fälle: mit und ohne erlaubten Wiederholungen. Sind Wiederholungen erlaubt, entspricht das einem Zurücklegen im Urnenmodell.
Beispiel im Urnenmodell
Für die Menge der drei Buchstaben A, und C gibt es insgesamt 6 mögliche Kombinationen, wenn Wiederholungen erlaubt sind, wenn also ein gezogener Buchstabe wieder zurück in die Urne gelegt wird:
- A A
- A B (BA wäre das Gleiche)
- A C (CA wäre das Gleiche)
- B B
- B C (CB wäre das Gleiche)
- C C
Formeln
- Anzahl an Kombinationen = n+k-1 über k
- Anzahl an Kombinationen = (n+k-1)/[(n-1)!·k!]
Legende
- n = Anzahl der Elemente in der Grundmenge
- k = Anzahl der ausgewählten Elemente
- ! = mathematisch die 👉 Fakultät
Zahlenbeispiel
- Einsetzen:
- 3+2-1 über 2
- 4 über 2
- "Über" rechnet man so:
- 4! geteilt durch (4-2)!2!
- Ausrechnen:
- 1·2·3·4 geteilt durch 2!2!
- 24:4=6
- Es gibt 6 Kombinationen mit Wiederholungen.
- Siehe auch unter 👉 n über k