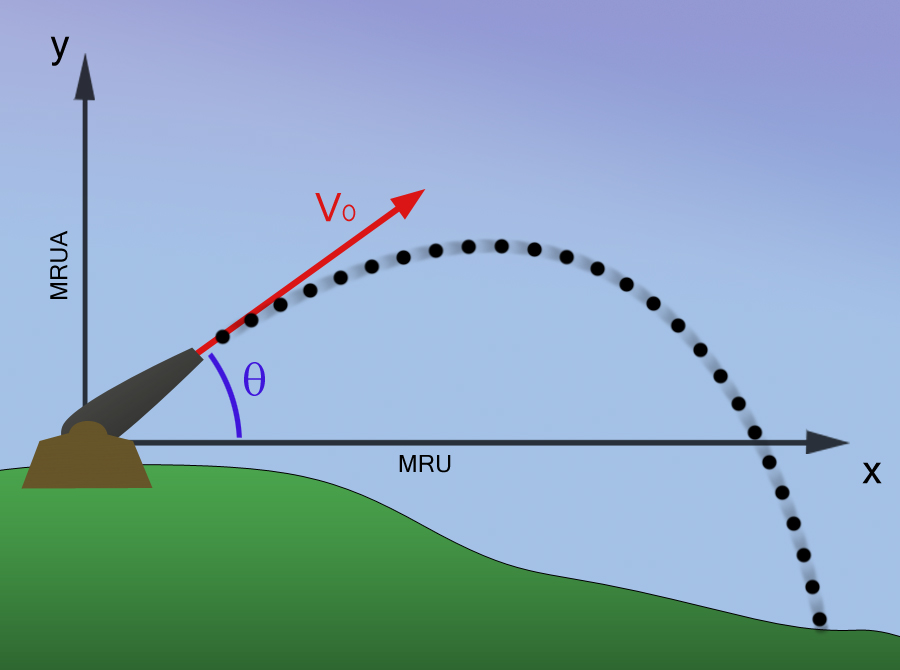
Wurfparabel
Physik
© 2016
- 2025
Definition
Die Wurfparabel ist die Flugbahn, die ein Körper - das sogenannte Projektil - beim Wurf in einem homogenen Schwerefeld beschreibt. Homogen meint hier, dass die Schwerkraft überall gleich stark ist und überall in die gleiche Richtung wirkt. Das trifft zum Beispiel auf Steine und bodennah fliegende Geschosse. Auf Raketen in großen Höhen, auch im antriebslosen Fall, trifft das nicht mehr zu. Dort muss man die sich ändernde Schwerkraft ständig in ihren wechselnden Werten anpassen.
ZITAT:
Galileo Galilei, 1639: "Man hat beobachtet, dass Wurfgeschosse eine gewisse Curve beschreiben; dass letztere aber eine Parabel sei, hat Niemand gelehrt." [1]
Galileo Galilei, 1639: "Man hat beobachtet, dass Wurfgeschosse eine gewisse Curve beschreiben; dass letztere aber eine Parabel sei, hat Niemand gelehrt." [1]
Formeln
- vx = v0·cos(θ)
- vy = v0·sin(θ) + g·t
- sx = vx · t
- sy = v0·sin(θ)·t + 0,5gt²
- w = v₀²·sin(2α)/g
- h = v₀²·sin²θ/(2g)
Legende
- vx = Geschwindigkeit in waagrechter Richtung, ist immer gleich groß
- v0 = Geschwindigkeit beim Start
- vy = Geschwindigkeit in senkrechter Richtung zum Zeitpunkt t
- sx = Zurückgelegte waagrechte Strecke zur Zeit t
- sy = Höhe über dem Abflugpunkt zur Zeit t
- g = Erdbeschleunigung (etwa 9,81 m/s^2)
- θ = Höhenwinkel, unter dem geworfen wird; θ=0° heißt waagrecht, θ=90° senkrecht nach oben
- w = 👉 Wurfweite
- h = 👉 Steighöhe
- · = 👉 Malzeichen
- / = 👉 Geteiltzeichen
Vorzeichen
- Bewegungen, Beschleunigungen, Wegstrecken, Winkel nach oben: positiv
- Bewegungen, Beschleunigungen, Wegstrecken, Winkel nach unten: negativ
Geltungsbereich
- Die Formeln oben gelten nur für reibungsfreie Würfe.
- Man vernachlässigt also den Luftwiderstand.
- Die Formeln gelten nur für eine eben gedachte Erdoberfläche.
- Will man die Erdrundung mit beachten, braucht man andere Formeln.
- Die Formeln gelten nur für Bereiche nahe der Erdoberfläche.
- Ein Sturz, etwa vom Mond, kann damit nicht berechnet werden.
Beispiele
Bleikugelflug
Pilot der Drohne war Sebastian Schieferdecker. Er führte im Wesentlichen auch die Auswertung des Filmmaterials durch.
.png)
Die mit Hand abgeworfene Bleikugel folgte grob der Bahn einer Parabel. Die Auswertung des Filmmaterials war aber nicht ganz einfach.
Schwierig war es, die horizontale Entfernung des Scheitelpunktes vom Abworfort einigermaßen gut abzuschätzen. Siehe mehr dazu unter 👉 Wurfparabel (Bleikugelflug)
Raketenflug
Dieser Versuch wurde durchgeführt und ausgewertet von Jonathan Lebherz.
Die abgefeuerte Streichholzrakete folgte in ihrem Flug recht gut einer Wurfparabel. Daraus lässt zwei Szenarien zu: a) die Rakete kompensierte mit ihrem Antrieb während des Fluges den Einfluss des Luftwiderstandes oder b) weder der Raketenantrieb nach dem Start noch der Luftwiderstand hatten einen nennenswerten Einfluss auf die Flugbahn.
Einzelne Punkte wurden mit Hilfe von vorher aufgestellten senkrechten Stäben von etwa 2 Metern Länge und eine einer anschließenden Videoauswertung des Raketenflugs bestimmt: (0|0,9) (1|1,56) (2|1,84) (3|1,85) (4|1,45) (5|0,75) (5,5|0). Der x-Wert steht dabei für die horizontale Distanz zum Abschusspunkt in Metern und der y-Wert für die senkrechte Höhe über dem Boden in Metern. Der Versuch wurde durchgeführt, dokumentiert und ausgewertet von Jonathan Lebherz. Zur mathematischen Auswertung der Flugparabel der Rakete siehe auch 👉 Wurfparabel (Raketenflug)
Fußnoten
- [1] Galilei über die Wurfparabel: Galileo Galilei: Unterredungen und mathematische Demonstrationen über zwei neue Wissenszweige, die Mechanik und die Fallgesetze betreffend. In: Ostwald’s Klassiker der exakten Wissenschaften.Leipzig 1890, 1904, 1891. Nachdruck: Darmstadt: Wissenschaftliche Buchgesellschaft, 1964. S.140-160.