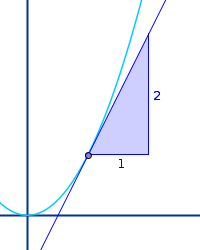
Parabelsteigung
An einem Punkt
Definition
Eine Parabel als Funktionsgraph hat an jedem Punkt eine andere Steigung. Am Scheitelpunkt ist die Steigung immer gleich 0. Links und rechts nach außen auf den Parabelästen wird der Graph dann immer steiler: der Betrag der Steigung nimmt zu. Das ist hier erklärt.
Definition einer Parabelsteigung
- Parabel meint hier: Graph einer quadratischen Funktion.
- Eine Parabel als Ganzes hat keine bestimmte Steigung.
- Aber jeder Punkt einer Parabel hat eine Steigung.
- Das ist die Steigung der Tangente an dem Punkt.
- Siehe auch Steigung in einem Punkt ↗
Berechnung einer Parabelsteigung
- Bilde die erste Ableitung f'(x) der Funktionsgleichung.
- Setze irgendeinen x-Wert in f'(x) ein.
- Das ist die Steigung an dem Punkt mit x.
- Mehr über Parabelsteigung berechnen ↗
Tipps
- Im Scheitelpunkt ist die Steigung 0 ↗
- Von links nach rechts bergauf: positive Steigung ↗
- Von links nach rechts bergab: negative Steigung ↗
Was ist der Öffnungsparameter?
In der allgemeinen Form der Parabelgleichung y = ax² + bx + c ist das kleine a der sogenannte Öffnungsparameter[1]. Dieser gibt an, wie stark gestreckt oder gestauch die Parabel ist. Je weiter entfernt der Wert von der 0 ist, desto gestreckter und damit auch umso steiler ist die Parabel. Lies mehr unter Öffnungsparameter ↗
Fußnoten
- [1] Lothar Papula: Mathematik für Ingenieure und Naturwissenschaftler. Ein Lehr- und Arbeitsbuch für das Grundstudium. Band 1. 14. Auflage, 2019. ISBN: 978-3-658-05619-3. Verlag Springer Vieweg. Dort die Seite 195.
