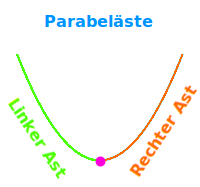
Parabeläste
Bedeutung | Beispiele
Basiswissen
Parabeln haben immer zwei Äste: sie kommen unter anderem als Graph von quadratischen Funktionen vor. Die Parabeln stehen dann immer senkrecht in einem xy-Koordinatensystem. Das ist hier kurz erklärt.
Die Parabel als Funktionsgraph
- Man hat eine quadratische Funktion wie z. B. => f(x)=x²
- Der Graph einer quadratischen Funktion heißt => Parabel
- Er hat einen linken Ast und einen rechten Ast.
- Zwischen den Ästen liegt der => Scheitelpunkt
Parabeläste als Symmetriehälften
- Der Graph einer quadratischen Funktion hat immer einen Scheitelpunkt.
- Der Scheitelpunkt ist der höchste oder tiefste Punkt der Parabel.
- Zieht man eine senkrechte Linie durch den Scheitelpunkt, dann ...
- hat man die Parabel in zwei symmetrische Hälften geteilt.
- Jede dieser Hälften ist ein Ast der Parabel.
- Es gibt einen linken Parabelast und ...
- es gibt einen rechten Parabelast.
- Siehe auch => Achsensymmetrie
Gehört der Scheitelpunkt zu einem der Äste?
- Das wird nicht einheitlich gehandhabt.
- Auf dieser Seite zählen wir den Scheitelpunkt nicht zu den Ästen.
- Eine Parabel bestünde demnach aus drei Abschnitten:
- Linker Ast, Scheitelpunkt und rechter Ast.
Welche Steigung haben die Parabeläste?
- Der Betrag der Steigung sagt, wie steil ein Graph an einem Punkt ist.
- Der Betrag der Steigung steigt mit der Entfernung vom Scheitelpunkt.
- Ein Ast für sich alleine ist entweder => streng monoton steigend
- oder er ist => streng monoton fallend
- Siehe auch => Parabelsteigung
Welche Krümmung haben Parabeläste?
- Eine bestimmte Parabel ist entweder ...
- überall rechts oder überall linksgekrümmt.
- Beide Parabeläste haben also immer dieselbe Krümmung: rechts oder links.
- Eine nach oben geöffnete Parabel ist immer und überall => linksgekrümmt
- Eine nach unten geöffnete Parabel ist immer und überall => rechtsgekrümmt
Haben die Äste besondere Punkte?
- Ein einzelner Parabelast hat keine Hoch- oder => Tiefpunkte
- Ein einzelner Parabelast hat keine => Sattelpunkte
- Ein einzelner Parabelast hat keine => Wendepunkte
- Der Scheitelpunkt ist aber immer ein => Extrempunkt
Weitere Bedeutungen von Parabel
- Das Wort Parabel gibt es in mindestens zwei ähnlichen Bedeutungen:
- In der Geometrie gibt es die => Parabel als Ortslinie
- In der Analysis gibt es Parabeln als Graphen ganzrationaler Funktionen
- In der Schulmathematik meint Parabel an sich aber meistens nur ...
- den Graphen einer quadratischen Funktion.
- Siehe auch => Parabel
