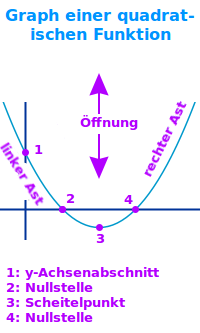
Graph einer quadratischen Funktion
Parabel
Basiswissen
Jede Funktion, die man so umformen kann, dass sie die Form f(x)=ax²+bx+c hat nennt man eine quadratische Funktion. Der Funktionsgraph einer solchen Funktion ist immer eine Parabel. Sie hat einige feste Eigenschaften. Diese werden hier kurz vorgestellt.
Eigenschaften
◦ Eine solche Parabel hat immer genau einen => Scheitelpunkt
◦ Eine solche Parabel hat immer genau zwei => Parabeläste
◦ Eine solche Parabel hat immer eine => Parabelöffnung
Gehört jede Parabel zu einer quadratischen Funktion?
◦ Nein.
◦ Es gibt auch Parabeln, die quer im Koordinatensystem liegen.
◦ Sie gehören zwar zu einer Zuordnung, aber nicht zu einer Funktion.
◦ Ein Beispiel dazu steht unter => nach links geöffnet
Was ist der Scheitelpunkt?
◦ Das ist der höchste der tiefste Punkt der Parabel.
◦ Der Scheitelpunkt kann ein Hoch- oder ein Tiefpunkt sein.
◦ Lies mehr dazu unter => Scheitelpunkt einer Parabel
Was sind die Parabeläste?
◦ Eine Parabel hat einen linken und einen rechten Ast.
◦ Das sind die Teile des Graphen links und rechts vom Scheitelpunkt.
◦ Lies mehr dazu unter => Parabeläste
Gibt es immer einen y-Achsenabschnitt?
◦ Ja.
◦ Das gilt für alle Parabeln als Graphen einer quadratischen Funktion.
◦ Der y-Achsenabschnitt ist der y-Wert, bei dem die Parabel durch die y-Achse geht.
◦ Lies mehr dazu unter => y-Achsenabschnitt einer Parabel
Was ist die Parabelöffnung?
◦ Die Öffnung gibt an, ob die Äste nach oben oder unten gehen.
◦ Man lässt die Äste dabei gedanklich im Scheitelpunkt beginnen.
◦ Gehen sie von dort aus nach oben, ist die Parabel => nach oben geöffnet
◦ Gehen sie nach unten, ist die Parabel => nach unten geöffnet
Was meint Streckung oder Stauchung?
◦ Das meint üblicherweise, wie schmal und steil ...
◦ oder wie flach und dick eine Parabel aussieht.
◦ Lies mehr dazu unter => Parabelstreckung
Was kann man über die Nullstellen sagen?
◦ Nullstellen sind x-Werte auf der x-Achse.
◦ Es sind diejenigen x-Werte bei denen die Parabel die x-Achse schneidet.
◦ Eine Parabel kann - muss aber keine - Nullstellen haben.
◦ Siehe mehr dazu unter => Nullstellen von quadratischen Funktionen
Was sind Transformationen einer Parabel?
◦ So bezeichnet man Veränderung der Parabelform oder Lage.
◦ Ändert man die Funktionsgleichung f(x), kann man eine Parabel transformieren.
◦ Man kann sie strecken, stauchen oder verschieben.
◦ Mehr unter => Parabeltransformationen
