Orthogonal
90°-Winkel
Ein Objekt heißt Orthogonal zu einem anderen, wenn sich die beiden Objekte mit einem 90°-Winkel berühren. Eine Hauswand steht orthogonal auf einer anderen Wand, wenn beide rechtwinklig zueinander sind. Ortho heißt recht und gonal so viel wie mit Ecken in Beziehung stehend. Siehe auch => Orthogonalität prüfen
Etwas mit 90°-Winkel
Eine Gerade, Strecke oder Ebene kann eine Orthogonale zu etwas anderem sein. Das meint dann, dass sie mit einem 90°-Winkel (also senkrecht) auf etwas anderes trifft. Eine Gerade kann zum Beispiele eine Orthogonale von einer anderen Geraden sein. Man unterscheidet dabei 2D- und 3D-Koordinatensysteme. => Ganzen Artikel lesen …
… Fremdwort für ein => Rechteck
Physik
Orthograd heißt wörtlich so viel wie in die rechte, richtige Richtung [1] voranschreitend [2]. In der Medizin kann es zum Beispiel heißen, in Richtung der Röntgentrahlen. [3] Der Anthropologe Terrence W. Deacon bezeichnet mit orthograd die Einhaltung einer Richtung von Veränderungen auf eine natürliche, spontane Weise, ohne dass dazu äußere Einflüsse nötig sind. [4] => Ganzen Artikel lesen …
90°
Orthogonalität heißt auch Deutsch Rechtwinkligkeit. Zwei Dinge sind rechtwinklig oder Orthogonal zueinander, wenn sie einen 90°-Winkel haben oder einschließen. Das kann zum Beispiel zutreffen auf Dreiecke (rechtwinklig), auf Vektoren, Geraden oder auch Ebenen. Lies mehr unter => Orthogonalität prüfen
… meint dasselbe wie nicht rechtwinklig, siehe unter => keine rechten Winkel
Physik
Sind zwei beliebige Basisvektoren zueinander immer senkrecht, also Orthogonal (90° Winkel), so nennt man alle Vektoren die so einen Vektorraum aufspannen gemeinsam eine Orthogonalbasis. [1] Dabei dürfen die einzelnen Basisvektoren unterschiedlich lang sein. Müssen alle Basisvektoren zusätzlich noch die Länge 1 haben, spricht man von einer => Orthonormalbasis
Physik
Eine Abbildung heißt orthogonal, wenn sie das Skalarprodukt erhält [1], das heißt, das Ergebnis des Skalarprodukts zwier Vektoren hat vor der Abbildung denselben Wert wie nach der Abbildung. => Ganzen Artikel lesen …
… Gerade senkrecht auf Punkt von Graph => Normalengleichung aufstellen
… Gerade senkrecht auf Punkt von Graph => Normalengleichung aufstellen
Vektorrechnung
Zwei Ebenen sind genau dann orthogonal zueinander, wenn ihre Normalnvektoren zueinander orthogonal sind. Ob die zwei Normalenvektoren zueinander senkrecht sind kann man mit Hilfe des Skalarproduktes überprüfen (muss Null ergeben). Mehr zum Hintergrund, siehe unter => Normalenform der Ebene
… ist nicht linear, warum steht unter => senkrechte Gerade
… ist nicht linear, warum steht unter => senkrechte Gerade
… ist nicht linear, warum steht unter => senkrechte Gerade
3D-Geraden
Zwei Geraden in einem xy-Koordinatensystem stehen orthogonal zueinander, wenn sie in ihrem Schnittpunkt einen 90°-Winkel bilden. Zwei Geraden in einem xyz-Koordinatensystem stehen orthogonal zueinander, wenn das Skalarprodukt ihrer Richtungsvektoren 0 ergibt. Beide Fälle sind hier kurz erklärt. => Ganzen Artikel lesen …
Matrizen
Alle nxn (quadratisch) Matrizen für die die folgenden Bedingungen gelten bilden gemeinsam eine orthogonale Gruppe: A⁻¹=Aᵀ und AAᵀ = AᵀA. Ferner gilt noch dass die Determinante von A den Wert 1 hat. Aᵀ die zu A transonierte Matrix. Und A⁻¹ ist die zu A inverse Matrix. Siehe auch => Matrizenrechnung
Definition
Eine Matrix M heißt orthogonal, wenn sie quadratisch ist (gleich viele Spalten wie Zeilen) und wenn zusätzlich gilt: ihr Mᵀ·M=E sowie M·Mᵀ=E. Dabei ist M die Matrix, Mᵀ die dazu transponierte Matrix, E die Einheitsmatrix. Die Inverse einer orthogonalen Matix ist gleich ihrer Inversen. [1] Eine orthogonale Matrix erhält das Standardskalarprodukt. Das heißt, dass das Skalarprodukt von zwei Vektoren durch eine Multiplikation mit der Matrix nicht verändret wird. [2] => Ganzen Artikel lesen …
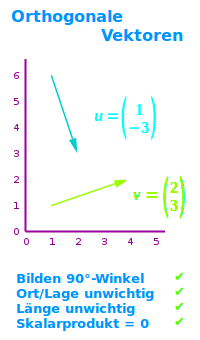Orthogonale Vektoren
90°-Winkel
Orthogonale Vektoren sind hier zwei oder mehr Vektoren, die zueinander orthogonal, das heißt rechtwinklich sind, also einen 90°-Winkel einschließen. Das Skalarprodukt solcher zueinander orthogonaler Vektoren ist immer 0. => Ganzen Artikel lesen …
Anleitung
Man hat einen Vektor oder auch zwei Vektoren gegeben und soll dazu einen weiteren Vektor angeben, der orthogonal, das heißt senkrecht, also im 90°-Winkel, zu den gegebenen Vektoren steht. Hier sind verschiedene Verfahren dazu kurz vorgestellt. => Ganzen Artikel lesen …
Anleitung
Die Vektoren (2|3|4) und (3|2|-3) sind zueinander orthogonal: immer dann - und auch nur dann - wenn das Skalarprodukt von zwei Vektoren genau 0 ergibt, dann sind die zwei Vektoren zueinander orthogonal, sie bilden dann also einen rechten Winkel. Das ist hier kurz mit Beispielen vorgestellt. => Ganzen Artikel lesen …
… ist nicht linear, warum steht unter => senkrechte Gerade
… ist nicht linear, warum steht unter => senkrechte Gerade
… Unüblicher Ausdruck für ein => rechtwinkliges Dreieck
Orthogonal heißt auf deutsch rechtwinklig oder mit-90-Grad-Winkel. Man spricht von Orthogonalen Geraden, Vektoren und Ebenen, aber nicht von orthogonalen Dreiecken. Bei Dreiecken heißt es => rechtwinkliges Dreieck
Orthogonales Trapez
Mindestens ein 90°-Winkel
Ein Trapez ist ein Viereck mit mindestens zwei parallelen Seiten. Die Seiten dürfen - müssen aber nicht - senkrecht aufeinander stehen. Senkrecht aufeinander heißt: mit einem 90°-Winkel. Gibt es in dem Trapez mindestens einen 90°-Winkel, heißt das Trapez auch rechtwinklig oder orthogonal. Siehe allgemein auch => Trapez
Verfahren
Dreiecke für sich oder Strecken, Geraden oder Vektoren zueinander können orthogonal sein. Orthogonal heißt auf Deutsch rechtwinklig. Um die Orthogonanlität zu überprüfen, gibt es verschiedene Verfahren. Diese sind hier kurz vorgestellt. => Ganzen Artikel lesen …
Überprüfen
Zwei Vektoren und auch zwei Geraden sind genau dann senkrecht zueinander, wenn ihr Skalarprodukt genau 0 ergibt. Für Ebenen ist diese Bedingung aber nicht hinreichend. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… in der Vektorrechnung => Orthogonalität über Skalarprodukt
- => Orthogonalität über Skalarprodukt
… „Senkrechtaufeinanderheit“, siehe unter => orthogonale Geraden
… siehe unter => Orthogonalbasis
Unterschied
Man bohrt ein Loch senkrecht in den Boden oder man bringt eine Balken orthogonal zu einer Dachfläche: hier wird erklärt, wann die Worte dasselbe und wann sie etwas unterschiedliches bedeuten. => Ganzen Artikel lesen …
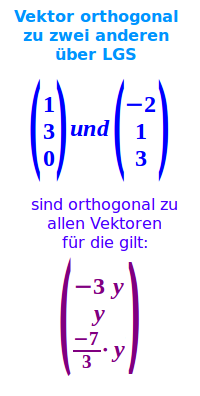Vektor orthogonal zu zwei anderen über LGS
Beispielrechnung
LGS meint hier: Lineares Gleichungssystem. Gegeben sind zwei Vektoren. Die Vektorkoordinaten des einen Vektors a sind zum Beispiel 1, 3 und 0. Die Koordinaten des anderen Vektors b sind -2, 1 und 3. Gesucht sind alle Vektoren, die senkrechten auf jeweils beiden gegebenen Vektoren stehen. => Ganzen Artikel lesen …
… stehen senkrecht aufeinander, Skalarprodukt ist Null, mehr unter => Orthogonale Vektoren
… stehen senkrecht aufeinander, Skalarprodukt ist Null, mehr unter => Orthogonale Vektoren
… Gerade senkrecht auf Punkt von Graph => Normalengleichung aufstellen
… 90°-Winkel zwische den Geraden => orthogonale Geraden
