A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 9 Ω
Das Banner der Rhetos-Website: zwei griechische Denker betrachten ein physikalisches Universum um sie herum.

Orthogonale Vektoren

90°-Winkel

© 2016 - 2025


Basiswissen｜ Was meint orthogonal?｜ Müssen sich die Vektoren dazu berühren?｜ Wie erkennt man orthogonale Vektoren?｜ Was ist ein Normalenvektor?


Basiswissen


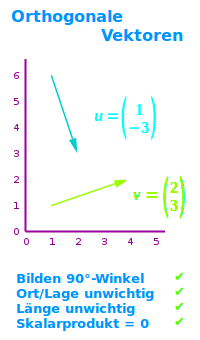
Orthogonale Vektoren sind hier zwei oder mehr Vektoren, die zueinander orthogonal, das heißt rechtwinklich sind, also einen 90°-Winkel einschließen. Das Skalarprodukt solcher zueinander orthogonaler Vektoren ist immer 0.



Bildbeschreibung und Urheberrecht
Die Vektoren u und v kann man so verschieben, dass sie an ihrem Schnittpunkt einen 90°-Winkel bilden. Alle Vektoren, mit denen das geht, nennt man zueinander orthogonal. Orthogonal heißt auf deutsch auch rechtwinklig zueinander.☛


Was meint orthogonal?


  • Orthogonal heißt auf so viel wie rechtwinklig.
  • Zwei Dinge sind orthogonal zueinander, wenn sie einen 90°-Winkel bilden.
  • Bei Vektoren meint ortogonal, dass sie rechtwinklig zueinander sind.

Müssen sich die Vektoren dazu berühren?


  • Nein. Vektoren haben ohnehin keine feste Lage.
  • Hat man Vektoren gezeichnet, die sich nirgends berühren, dann ...
  • kann man sie gedanklich so lange (parallel) verschieben, bis sie sich berühren.
  • Man darf sie beim Verschieben allerdings nicht drehen.

Wie erkennt man orthogonale Vektoren?


  • Formal überprüft man die Orthogonalität über das Skalarprodukt.
  • Das Skalarprodukt von zwei orthogonalen Vektoren ergibt immer Null.
  • Umgekehrt gilt auch: ist das Skalarprodukt Null, sind die Vektoren orthogonal zueinander.
  • Ausnahme: Keiner der Vektoren darf der Nullvektor (0|0|0) sein Nullvektor ↗

Was ist ein Normalenvektor?


  • Ein Vektor, der senkrecht mit 90° auf einem anderen Vektor steht ...