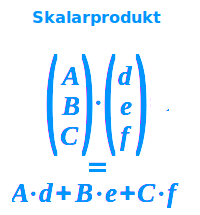Skalarprodukt

Übersicht

Definition · Skalarprodukt berechnen · Das Skalarprodukt und Winkel (Geometrie) · Das Skalarprodukt ist genau 0 · Das Skalarprodukt ist > 0 · Das Skalarprodukt ist < 0 · Das Skalarprodukt und der genaue Winkel · Das Skalarprodukt und Längen (Physik) · Schreibweisen für das Skalarprodukt · Was ist ein Skalar? · Was heißt hier Produkt? · Rechengesetze zum Skalarprodukt · Das Skalarprodukt und Kommutativgesetz · Das Skalarprodukt und das Assoziativgesetz · Das Skalarprodukt und das Distributivgesetz · Fußnoten

Definition

Der Vektor (1 2 3) skalar multipliziert mit dem Vektor (2 2 2) gibt als Ergebnis die Zahl 12: das Skalarprodukt von zwei Vektoren, auch inneres Produkt genannt ist als Ergebnis immer eine reelle Zahl (und nicht etwa wieder ein Vektor). Das Skalarprodukt hat verschiedene anschauliche Bedeutung und spielt eine wichtige Rolle in der Vektorrechnung.

Bildbeschreibung und Urheberrecht — Man schreibt zwei Vektoren senkrecht nebeinander. Dann werden alle Zahlen auf derselben Höhe miteinander multipliziert. Die Ergebnisse dieser Multiplikation werden dann alle aufaddiert. Das Ergebnis ist das gesuchte Skalarprodukt.☛

Skalarprodukt berechnen

Das Skalarprodukt ist vergleichsweise einfach zu berechnen. Das Skalarprodukt der Vektoren (1 2 3) und (5 5 5) ist 1·5 + 2·5 + 3·5, ausgerechnet also die Zahl 30. Man multipliziert zunächst alle Vektorkoordinaten, die an derselben Stelle innerhalb einer Klammer stehen. Dann addiert man diese Produkte alle auf, bildet also die Summe. Diese Summe am Ende der Rechnung ist das Skalarprodukt. Allgemein gilt:

FORMEL

(a b c)·(A B C) = a·A + b·B + c·C

BEISPIELE

(4 4 4)·(0 1 2) = 4·0 + 4·1 + 4·2 = 12

(4 1 4)·(1 5 1) = 4·1 + 1·5 + 4·1 = 13

(4 0 6)·(2 9 1) = 4·2 + 0·9 + 6·1 = 14

Die Zahlen innerhalb der Klammern nennt man die Vektorkoordinaten. Wenn in einer Rechnung negative und positive Vektorkoordinaten gleichzeitig vorkommen, kann das Skalarprodukt am Ende auch zu 0 oder einer negativen Zahl werden (siehe weiter unten). Mehr zur Berechnung des Skalarproduktes steht im Artikel Skalarprodukt berechnen ↗

Das Skalarprodukt und Winkel (Geometrie)

Das Ergebnis des Skalarprodukts gibt einen ersten Hinweis darauf, welchen Winkel zwei Vektoren miteinander bilden. Stellt man sich die zwei Vektoren wie die zwei Striche eines großen Buchstaben V vor, dann ist der gemeinte Winkel immer der kleinere Winkel zwischen den zwei Strichen. Nicht berücksichtigt wird dabei jedoch der Fall, dass einer der Vektoren oder beide Vektoren der Nullvektor (0 0 0) sind. Der Nullvektor hat keine Länge und kann deshalb auch nicht der Schenkel eines Winkels sein. Die folgenden Aussagen gelten also nur dann, wenn keiner der betrachteten Vektoren der Nullvektor ist. Je nach Ergebnis des Skalarproduktes kann man dann verschiedene Fälle unterscheiden.

Das Skalarprodukt ist genau 0

Wenn das Skalarprodukt von zwei Vektoren genau Null ergibt, dann stehen die zwei Vektoren genau senkrecht aufeinander, sie bilden also einen rechten Winkel. Man sagt auch, sie seien orthogonal zueinander. Siehe mehr im Artikel Orthogonalität über Skalarprodukt ↗

Das Skalarprodukt ist > 0

(4 0 5)·(2 0 3) = 23: wenn das Ergebnis des Skalarproduktes größer ist als Null, also eine positive Zahl, dann ist der Winkel zwischen den Vektoren immer ein spitzer Winkel. Spitz nennt man alle Winkel die größer als 0° und kleiner als 90° sind. Siehe auch spitzer Winkel ↗

Das Skalarprodukt ist < 0

(4 0 5)·(2 0 -3) = -7: wenn das Ergebnis des Skalarprodukes kleiner ist als Null, also eine negative Zahl, dann ist der Winkel zwischen den Vektoren immer ein stumpfer Winkel. Stumpf nennt man Winkel die größer als 90° und kleiner als 180° sind. Siehe mehr unter stumpfer Winkel ↗

Das Skalarprodukt und der genaue Winkel

Das reine Skalarprodukt, also das Zahlenergebnis der skalaren Multiplikation, gibt eine Auskunft darüber, ob der Winkel zwischen zwei Vektoren genau spitz, genau 90° oder stumpf ist. Es gibt aber auch eine Formel, mit der man den exakten Wert eines Winkels zwischen zwei Vektoren berechnen kann:

a·b = |a|·|b|·cos(alpha)

Dabei sind a und b je ein Vektor. |a| ist die Länge oder Betrag des Vektors a, entsprechend ist |b| die Länge oder der Betrag des Vektors b. Und alpha ist der kleinere der zwei von a und b eingeschlossenen Winkel. Stellt man diese Gleichung um nach alpha, kann man den Winkel zwischen zwei Vektoren direkt ausrechnen. Siehe mehr unter Winkel über Skalarprodukt ↗

Das Skalarprodukt und Längen (Physik)

Abgesehen von der Deutung des Skalarproduktes zweier Vektoren a und b hinsichtlich des Winkels, gibt es noch eine zweite, ganz andere anschauliche Deutung: Das Skalarprodukt ist immer gleich dem Produkt der Länge des Vektors a mit der Länge der Projektion von b auf a. Diese Bedeutung ist der Schlüssel zum Verständnis vieler Formeln der Physik (z. B. Kraft und Arbeit, Vektoranalysis). Siehe mehr unter Skalarprodukt anschaulich ↗

Schreibweisen für das Skalarprodukt

Als Platzhalter für Vektoren werden normalerweise lateinische Kleinbuchstaben verwendet. Dass sie für Vektoren stehen sollen, kann man auf zwei Arten deutlich machen: man setzt einen kleinen Rechtspfeil über den Buchstaben. Oder aber man schreibt den Buchstaben kursiv (englisch: italic). Für das Skalarprodukt gibt es verschiedene Schreibweisen. Wichtig ist, eine Verwechslung mit dem Vektor- oder Kreuzprodukt zu vermeiden. Für das Skalarprodukt sind die folgenden Schreibweisen typisch.

𝑣⋅𝑤

𝑣∘𝑤

𝑣∙𝑤

(𝑣,𝑤)

⟨𝑣|𝑤⟩

Was ist ein Skalar?

In der Mathematik meint Skalar so viel wie reelle Zahl ↗

Ein Vektor, eine Matrix^[1] oder eine komplexe Zahl^[2] sind keine Skalare.

Skalare sind Zahlen wie: 3; -0,5 oder ½

Siehe auch Skalar ↗

Was heißt hier Produkt?

Man kann Vektoren auf verschiedene Weisen miteinander multiplizieren. Dabei kann das Ergebnis ein Vektor oder auch nur eine Zahl sein. Sollen zwei Vektoren so multipliziert werden, dass das Ergebnis ist ein Zahl ist, so nennt man sowohl das Ergebnis wie auch dem Malterm mit den zwei Vektoren das Skalarprodukt^[3].

Rechengesetze zum Skalarprodukt

Werden in der Mathematik Rechenarten neu eingeführt, wird meistens auch betrachtet, inwiefern die drei grundlegenden Rechengesetzte, nämlich das Kommutativgesetz, das Assoziativgesetz und das Distributivgesetz gelten.

Das Skalarprodukt und Kommutativgesetz

Die skalare Multiplikation ist kommutativ:

Vektor a mal Vektor b ist dasselbe wie Vektor b mal Vektor a skalar multiplziert.

Siehe auch Skalarprodukt aus drei Vektoren ↗

Das Skalarprodukt und das Assoziativgesetz

Die skalare Multiplikation ist nicht assoziativ:

Man betrachte als Beispiel die drei identischen Vektor a, b und c mit den Komponenten (1 2 3).

a·b gäbe eine Zahl. Diese Zahl würde dann mit c multipliziert.

Damit wäre der zweite Malpunkt aber keine skalare Multiplikation mehr.

Denn: Zahl mal Vektor gibt wieder einen Vektor, siehe auch Zahl mal Vektor ↗

Das Skalarprodukt von drei Vektoren ist nicht definiert ↗

Das Skalarprodukt und das Distributivgesetz

Die skalare Multipliaktion ist distributiv:

Die drei identischen Vektoren a, b und c hätten beispielhaft die Komponenten: (1 2 3)

Dann müsste gelten: a·(b+c) = a·b + a·c

a·(b+c) gibt ausgerechnet genau: 28

Auch a·b+a·c gibt genau 28.

Siehe auch Distributivgesetz ↗

Fußnoten

[1] Eine Matrix ist ein Rechenobjekt, das man als Tabelle darstellen kann. Man kann solche Matrizen addieren, subtrahieren und auch multiplizieren (nicht aber dividieren). Eine Matrix ist niemals ein Skalar. Siehe auch Matrix ↗

[2] Komplex nennt man Zahlen wie zum Beispiel 4+2i. Solche Zahlen können auch abseits der Zahlengeraden liegen. Auch solche Zahlen sind keine Skalare. Siehe auch Komplexe Zahl ↗

[3] Skalarprodukt ist wie auch das Wort Produkt doppeldeutig. So nennt man sowohl die Malaufgabe 3·4 ein Produkt, wie auch das Ergebnis, die Zahl 12. Möchte man dazwischen unterscheiden, so spricht man vom Produktterm (3·4) und dem Produktwert (12). Siehe mehr unter Produkt ↗