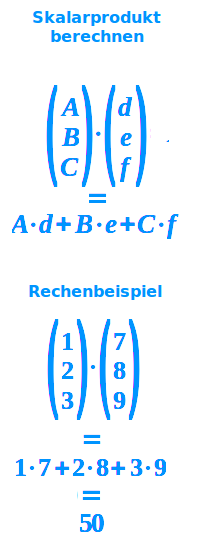
Skalarprodukt berechnen
Formel
© 2016
- 2025
Basiswissen
Die Vektoren (1|3|5) und (2|4|6) haben das Skalarprodukt 1·2 + 3·4 + 5·6 was ausgerechnet 44 gibt: man multipliziert alle entsprechenden Komponenten und addiert dann die so entstandenen Produkte auf. Das ist hier kurz allgemein formuliert.
Formel
- Ein Vektor besteht aus Komponenten.
- Das sind die Zahlen, die senkrecht übereinander stehen.
- Ein erster 3D-Vektor hätte z. B. die Komponenten A, B und C.
- Ein anderer 3D-Vektor hätte z. B. die Komponenten d, e und f.
- Dann ist das Skalarprodukt: Ad + Be + Cf
Rechenbeispiel
- Man hat den Vektor mit den Komponenten 1; 2 und 3.
- Man hat einen Vektor mit den Komponenten 7; 8 und 9.
- Skalarprodukt = 1·7 + 2·8 + 3·9 = 7 + 16 + 27 = 50
- Zur Bedeutung, lies unter 👉 Skalarprodukt