ℜ
Physik Chemie Grundschule Mathematik I Mathematik II Wissen
Kurze Worte Worte nach Alter Terme Rechner
Mathfeed Physfeed Philfeed
Das Lexikon Die Mission Die Autoren Copyright Impressum
Physik Nachhhilfe 5-10 Physik Nachhilfe 11-13 Chemie Nachhilfe 5-13 Mathe Nachhilfe 5-8 Mathe Nachhilfe 9-10 Mathe Nachhilfe 10-13
☰
1: Biquadratisch

Mit Quadraten von Quadraten

„Bi“ heißt soviel wie „zwei“ oder „doppelt“: ein Biquadrat ist ein Quadrat von einem Quadrat. (x²)² wäre also ein Biquadrat, oder kurz x^4. (Das Dach ^ meint „hoch“.) Das ist hier weiter erklärt. => Ganzen Artikel lesen …
2: Biequadratisch

… mit x^4 und Siehe unter => biquadratisch
3: Biquatratisch

… mit x^4 und Siehe unter => biquadratisch
4: Quadratisch

Geometrie | Gleichung | Funktion

Bei einem Rechteck meint quadratisch, dass alle vier Seiten gleich lang sind. Bei Funktionen und Gleichungen meint quadratisch, dass (mindestens) ein x-Quadrat irgendwo vorkommt. => Ganzen Artikel lesen …
5: Bestimmung der Nullstellen biquadratischer Funktionen

… siehe => Nullstellen von biquadratischen Funktionen bestimmen
6: Biquadratisch Funktionen NS berechnen

… siehe => Nullstellen von biquadratischen Funktionen bestimmen
7: Biquadratisch Funktionen NS bestimmen

… siehe => Nullstellen von biquadratischen Funktionen bestimmen
8: Biquadratisch Funktionen NS finden

… siehe => Nullstellen von biquadratischen Funktionen bestimmen
9: Biquadratisch Funktionen Nullstellen bestimmeni

… siehe => Nullstellen von biquadratischen Funktionen bestimmen
10: Biquadratisch Funktionen Nullstellen finden

… siehe => Nullstellen von biquadratischen Funktionen bestimmen
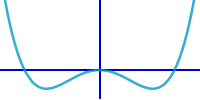11: Biquadratische Funktion

f(x) = ax^4 + bx^2 + c

Eine Funktion mit x hoch 4 und x hoch 2 nennt man biquadratisch. Diese Funktion und ihre Berechnungen werden hier kurz vorgestellt. => Ganzen Artikel lesen …
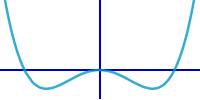12: Biquadratische Funktion ableiten

Zum Beispiel f(x) = 2x^4-5x^2+6 ableiten gibt f'(x) = 8x³-10x

Als biquadratisch Funktion bezeichnet man eine ganzrationale Funktion vierten grades (quartische Funktion) mit ausschließlich geraden Exponenten von x. Eine biquadratische Funktion hat die allgemeine Form f(x) = ax^4 + bx^2 + c. Durch Umformung kann man jede biquadratische Funktion in diese Form bringen. Sie kann dann mit Hilfe der Faktor- und der Potenzregel abgeleitet werden. => Ganzen Artikel lesen …
13: Biquadratische Funktionen

Beispiele

f(x) = 2x⁴ - 8x² + 16 - bei einer biquadratischen Funktion gibt es im Funktionsterm ein x⁴ sowie immer auch ein x². Daneben kann es - muss aber nicht - noch ein absolutes Glied geben, das heißt eine Zahl ohne x. Hier stehen einige Beispiele. => Ganzen Artikel lesen …
14: Biquadratische Gleichung

Definition

0 = ax^4 + cx^2 + e - jede Gleichung, die man in diese Form umformen kann nennt man biquadratisch: es gibt immer ein Glied mit x hoch 4 und ein Glied mit x hoch zwei. Das ist hier ausführlich erklärt. => Ganzen Artikel lesen …
15: Biquadratische Gleichung lösen

… siehe unter => Biquadratische Gleichungen lösen
16: Biquadratische Gleichung lösen über Probieren

… siehe unter => Biquadratische Gleichungen über Probieren
17: Biquadratische Gleichung lösen über Substitution

… siehe unter => Biquadratische Gleichungen über Substitution
18: Biquadratische Gleichung über Probieren

… siehe unter => Biquadratische Gleichungen über Probieren
19: Biquadratische Gleichung über Substitution

… siehe unter => Biquadratische Gleichungen über Substitution
20: Biquadratische Gleichungen

Beispiele

0 = x^4 - 3x² + 3 ist eine typische biquadratische Gleichung: hier stehe verschiedene solche Gleichungen in einer Übersicht zusammengestellt. => Ganzen Artikel lesen …
21: Biquadratische Gleichungen lösen

Übersicht

0 = 2x⁴-10x²+12 ist eine sogenannte biquadratische Gleichung. Typische Lösungsverfahren sind Probieren sowie die sogenannte Substitution. Hier steht eine kurze Übersicht zu verschiedenen Lösungsverfahren. => Ganzen Artikel lesen …
22: Biquadratische Gleichungen lösen über Probieren

… siehe unter => Biquadratische Gleichungen über Probieren
23: Biquadratische Gleichungen lösen über Substitution

… siehe unter => Biquadratische Gleichungen über Substitution
24: Biquadratische Gleichungen über Probieren

Lösen

Biquadratische Gleichungen kann man als Alternative zur Substitutions-Methode oft auch schnell über Probieren lösen: irgendwelche Zahlen einsetzen und dann sehen ob die Gleichung aufgeht. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
25: Biquadratische Gleichungen über Substitution

Anleitung

0 = ax^4 + bx² + c - Gleichungen in dieser Grunform nennt man biquadratisch. Das übliche - aber nicht das einzige - Lösungsverfahren ist die Substitution. Dise ist hier Schritt-für-Schritt erklärt. => Ganzen Artikel lesen …
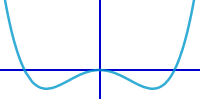26: Biquadratische Parabel

… der Graph von => biquadratische Funktion
27: Keine Biquadratische Gleichungen

Beispiele

Als biquadratisch bezeichnet man alle und nur solche ganzrationalen Gleichungen, die einem Term mit x⁴ und ein Glied mit x² haben, aber kein Glied mit x³. Erlaubt ist auch ein sogenannten absolutes Glied also eine reine Zahl ohne x. Hier stehen Beispiele für Gleichungen, die nicht biquadratisch sind. => Ganzen Artikel lesen …
28: NS berechnen biquadratische Funktionen

… siehe => Nullstellen von biquadratischen Funktionen bestimmen
29: NS bestimmen biquadratische Funktionen

… siehe => Nullstellen von biquadratischen Funktionen bestimmen
30: NS biquadratische Funktionen berechnen

… siehe => Nullstellen von biquadratischen Funktionen bestimmen
31: NS biquadratische Funktionen bestimmen

… siehe => Nullstellen von biquadratischen Funktionen bestimmen
32: NS biquadratische Funktionen finden

… siehe => Nullstellen von biquadratischen Funktionen bestimmen
33: NS finden biquadratische Funktionen

… siehe => Nullstellen von biquadratischen Funktionen bestimmen
34: Nullstellen-Bestimmung biquadratischer Funktionen

… siehe => Nullstellen von biquadratischen Funktionen bestimmen
35: Nullstellen berechnen von biquadratischen Funktionen

… siehe => Nullstellen von biquadratischen Funktionen bestimmen
Zur Startseite von Rhetos
Startseite
Impressum
© 2010-2023


Startseite Impressum Feedback © 2010-2023