Grenzwert
Analysis
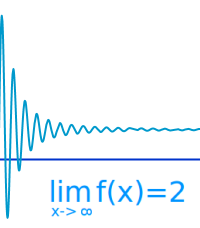
Von einem Grenzwert [1] oder Limes [7] spricht man bei Folgen, Reihen und Funktionen. Hier wird erklärt, wie der Grenzwert im Sinne der Mathematik exakt definiert ist. => Ganzen Artikel lesen …
Arten und Beispiele
Grenzwerte sind definiert für Folgen, Reihen und mathematische Funktionen. Hier werden verschiedene Arten wie uneigentliche, rechtsseitige und linksseitige Grenzwerte kurz vorgestellt. => Ganzen Artikel lesen …
Brennwert
🔥 Brennstoffe
Der Brennwert, oft in J pro Kilogrmam gibt an, wie viel chemische Energie in einem Brennstoff enthalten ist [1]. Dabei wird die Kondensationswärme mitgerechnet [4]. Der Brennwert ist damit immer höher als der etwas anders definierte Heizwert [2]. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
Bei Funktionen und in der Prozentrechnung
In der Prozentrechnung ist der Grundwert G das Ganze von dem man prozentuale Anteile denkt. Es gilt die Formel: Bei linearen Funktionen ist der Grundwert identisch mit dem y-Achsenabschnitt. Er spielt bei Textaufgaben eine Rolle. => Ganzen Artikel lesen …
… eine Regel zum Ausrechnen von Grenzwerten, Liste unter => Grenzwertsätze
… in der Betriebswirtschaft dasselbe wie das => Grenzprodukt
… Näherungsformeln für die Eulersche Zahl unter => e annähern
Funktionen
Man hat den Grahphen einer Funktion f(x). Nähert man sich mit den x-Werten langsam einem ganz bestimmten festgelegten x-Wert von links her an, dann entsteht ein sogenannten linksseitiger Grenzwert. Der linksseitige Grenzwert ist der y-Wert an den man immer besser herankommt. Analog gibt es auch einen rechtsseitigen Grenzwert. Siehe als Beispiel unter => linksseitiger Grenzwert
… Näherungsformeln für die Eulersche Zahl unter => e annähern
… Limes, siehe unter => Grenzwert (Funktion)
.png "Man setze den Finger gedanklichen irgendwo auf den Graphen. Geht man jetzt auf dem Graphen immer weiter Richtung positive x-Werte (nach rechts), dann wird der y-Wert dauerhaft immer näher an die 2 herankommen. Die Zahl 2 ist dann der Grenzwert von f(x) für x gegen unendlich.")
Grenzwert (Funktion)
Limes von f(x)
Von einem Grenzwert spricht man bei Folgen, Reihen und Funktionen. Hier geht es um den Grenzwert einer mathematischen Funktion wie zum Beispiel f(x)=1/x. => Ganzen Artikel lesen …
Der Limes in der Analysis
Ein Grenzwert ist immer ein Funktionswert, oft y-Wert genannt. Es ist ein Wert, an den sich ein Graph dauerhaft und immer mehr annähert. Lies mehr dazu unter => Grenzwert (Funktion)
… Näherungsformeln für die Eulersche Zahl unter => e annähern
… Näherungsformeln für die Eulersche Zahl unter => e annähern
Übersicht
Der Grenzwert gegen 0 oder gegen plus oder auch minus unendlich: eine häufig genutzte Art solche Grenzwerte zu bestimmen ist das Einsetzen von Zahlen in die Funktionsgleichung. Dazu steht hier eine Übersicht mit verschiedenen Fällen. => Ganzen Artikel lesen …
… für Funktionen und Graphen, siehe unter => Grenzwert
… Näherungsformeln für die Eulersche Zahl unter => e annähern
… Näherungsformeln für die Eulersche Zahl unter => e annähern
Funktionen
Der Grenzwert einer Funktion ist immer ein y-Wert. Um ihn für eine gegebene Funktionsgleich zu berechnen gibt es einige grundlegende Regeln die man nutzen kann. Diese sogenannten Grenzwertsätze sind hier kurz vorgestellt. => Ganzen Artikel lesen …
Stabile Verteilung
Stochastische Prozesse haben oft eine sogenannte stabile Verteilung. Kennt man die stochastische Matrix des Prozesses kann man darüber beurteilen, ob der Prozess irgendwann eine stabile Verteilung annimmt, die Verteilung sich also nicht mehr verändert. Das ist hier ausführlich erklärt. => Ganzen Artikel lesen …
… für Funktionen und Graphen, siehe unter => Grenzwert
Grenzwert innerer Funktion in äußere Funktion einsetzen
f(x) = (4+1/x)^x - wie verhält sich der Funktionswert, wenn x gegen plus unendlich geht? Für den Fall, dass es eine innere und eine äußere Funktion gibt (Verkettung), kann man die Frage schrittweise beantworten. Das wird hier kurz erklärt. Das Beispiel hier hat übrigens des Grenzwert plus unendlich. => Ganzen Artikel lesen …
… geht für x ⭢ unendlich gegen unteren Wert , siehe unter => Erschöpfungskurve
Linksseitiger Grenzwert
Von links kommend
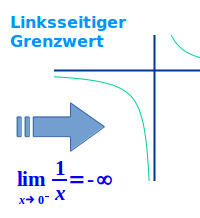
Der Graph der Funktion f(x)=1:x heißt Normalhyperbel. Der Graph geht durch den Punkt (-1|-1). Wenn man dort den Finger gedanklich auf den Graphen legt, kann man den Finger auf dem Graphen nach rechts bewegen. Dabei bewegt man sich von links kommend auf die y-Achse zu. Je näher man an die y-Achse herankommt, desto steiler und tiefer geht der Graph nach unten Richtung minus unendlich. Geht man also von links komment auf x=0 zu (die y-Achse), dann geht der y-Wert gegen minus unendlich. Man sagt: der linksseitige Grenzwert von f(x) für x gegen 0 ist minus unendlich. => Ganzen Artikel lesen …
… siehe unter => Grenzwerte über Probieren
Linksseitiger Grenzwert
Von rechts kommend
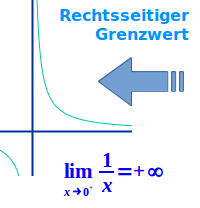
Der Graph der Funktion f(x)=1:x heißt Normalhyperbel. Der Graph geht zum Beispiel durch den Punkt (2|0,5). Wenn man dort den Finger gedanklich auf den Graphen legt, kann man den Finger auf dem Graphen nach links abfahren. Dabei bewegt man sich von rechts kommend auf die y-Achse zu. Je näher man an die y-Achse herankommt, desto steiler und höher geht der Graph nach oben Richtung unendlich. Geht man also von rechts komment auf x=0 zu (die y-Achse), dann geht der y-Wert gegen plus unendlich. Man sagt: der rechtsseitige Grenzwert von f(x) für x gegen 0 ist plus unendlich. => Ganzen Artikel lesen …
Uneigentlicher Grenzwert
Plus oder minus unendlich
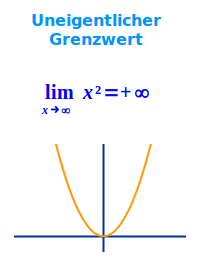
Wenn ein Funktionswert (analog auch der Wert einer Folge oder Reihe) in eine bestimmte Richtung von x-Werten irgendwann jeden beliebig großen Zahlenwert überschreitet und dann oberhalb dieses Zahlenwertes bleibt oder wenn für eine bestimmte Richtung von x-Werten jeder beliebig kleine y-Wert irgendwann einmal unterschritten wird und dann dauerhaft darunter bleibt, spricht man von einem uneigentlichen Grenzenwert. => Ganzen Artikel lesen …
… für die Wahrscheinlichkeitsrechnung, siehe => Satz von Moivre-Laplace
Die Binomialverteilung einer langen Bernoulli-Kette lässt sich mathematisch näherungsweise wie eine Normalverteilung behandeln. Dies besagt der Satz von Moivre-Lapalce (siehe oben). Mit Hilfe dieses Satzes lassen sich manche Rechnungen deutlich vereinfachen.
