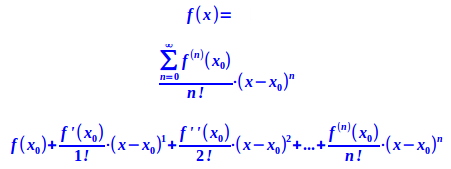Basiswissen

Was ist eine Taylor-Reihe?

• Eine Taylor-Reihe ist eine spezielle Potenzreihe ↗
  

• Das heißt: die Summanden sind immer ein Potenzterm ↗
  

• Die Taylor-Reihe besteht aus unendlich vielen Summanden ↗
  

• Die Taylor-Reihe wird immer für eine bestimmte Funktion erstellt.
  

• Wie die Taylor-Reihe erstellt wird, folgt einer bestimmten Formel ↗
  

Wozu sind Taylor-Reihen gut?

• Vor allem zur Berechnung von Näherungswerten für transzendente Funktionen ↗
  

• Das sind Funktionen wie cos, sin, tan, e^x und viele andere.
  

• Und auch zur Integration [Aufleitung] einiger schwieriger Funktionen.
  

• Ein Beispiel dazu ist die e^(x^2) aufleiten ↗
  

Wie bildet man eine Taylor-Reihe?

• Es müssen zwei Dinge gegeben sein: Eine Funktionsgleichung und eine Zahl a.
  

• Die Zahl a nennt man Entwicklungsstelle oder Entwicklungszentrum.
  

• Man nimmt die Funktion f(x) und berechnet ihren Funktionswert für x=0.
  

• Das war der erste Summand.
  

• Dann berechnet man f'(a), teilt es durch 1! und multipliziert alles mit (x-a)¹
  

• Das war der zweite Summand.
  

• Dann berechnet man f''(x), teilt es durch 2! und multipliziert alles mit (x-a)²
  

• Das war der dritte Summand.
  

• Dann berechnet man f'''(x), teilt es durch 3! und multipliziert alles mit (x-a)³
  

• Das war der vierte Summand.
  

• Und jetzt weiter so, bis vielleicht zum 5ten Summanden.
  

Wie deutet man eine Taylor-Reihe

• Es ist eine Pluskette aus einfachen Termen entstanden.
  

• In den Summanden taucht die Variable x auf.
  

• Sie ist dieselbe Variable wie die aus f(x).
  

• Wenn man Werte von f(x) berechnen will, kann ...
  

• man jetzt alternativ auch die Taylor-Reihe berechnen.
  

• Die Taylor-Reihe liefert eine gute Näherung für f(x).
  

• Je mehr Summanden man von der Taylor-Reihe benutzt, desto besser der Näherungswert ↗