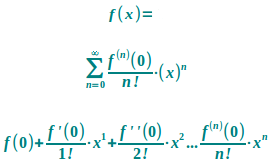Maclaurin-Reihe
Höhere Mathematik
Basiswissen
Eine Maclaurin-Reihe ist eine Näherungsformel für die Funktionswerte vieler Funktionen. Damit kann man zum Beispiel den Wert der Eulerschen Zahl oder auch Sinuswerte ganz auf die vier Grundrechenarten zurückführen. Das ist hier näher erklärt.
Wozu ist sie gut?
- man kann z. B. Sinuswerte rein über die vier Grundrechenarten bestimmen.
- Man kann viele Funktionen in unendliche Reihen umwandeln.
- Solche Reihen lassen sich immer leicht ab- und aufleiten.
- Die ursprünglichen Funktionen sind of schwer abzuleiten.
Wie erstellt man sie?
- Man hat am Anfang immer irgendeine Funktion f(x).
- Man leitet die Funktion f(x) mehrfach hintereinander ab.
- (Oft genügen drei bis fünf Ableitungen für Näherungswerte.)
- Aus f(x) und jeder seiner Ableitungen bildet man dann Terme ...
- und addiert diese Terme als Glieder einer Reihe (Summanden) auf.
- Der n-te Term wird so gebildet: [n-te Ableitung von f(0)] mal [x hoch n] geteilt durch [n Fakultät].
- Je mehr dieser Terme man aufaddiert, desto besser wird normalerweise die Näherung.
Funktioniert das immer?
Nein. Die Ausgangsfunktion muss auf jeden Fall mehrfach hintereinander ableitbar sein, um einigermaßen gute Näherungswerte zu kriegen. Auch muss der Funktionswert an der Stelle x=0 definiert sein. Und trotzdem gibt es noch Funktionen, die diese Bedingungen erfüllen und trotzdem nicht über die Maclaurinsche Reihe angenähert werden können. In der Regel benutzt man Formelsammlungen, die einem sagen, bei welchen Funktionen es funktioniert.
Was sind typische Beispiele aus Lehrbüchern?
- sin(x)
- cos(x)
- tan(x)
- e^x
Welche Funktionen gehen nicht?
- Wurzel aus x
- ln(x)
- 1/x
- etc.
Die Sinusfunktion als Beispiel
- Wir nehmen die Funktion f(x) = sin(x)
- (Die Winkel müssen im Bogenmaß (Rad) eingesetzt werden.)
- Wir bilden die ersten acht Ableitung und setzen für x die 0 ein:
- f(x) = sin(x) ⭢ wird mit x=0 zu 0
- f'(x) = cos(x) ⭢ wird mit x=0 zu 1
- f''(x) = -sin(x) ⭢ wird mit x=0 zu 0
- f'''(x) = -cos(x) ⭢ wird mit x=0 zu -1
- f''''(x) = sin(x) ⭢ wird mit x=0 zu 0
- f'''''(x) = cos(x) ⭢ wird mit x=0 zu 1
- f''''''(x) = -sin(x) ⭢ wird mit x=0 zu 0
- f'''''''(x) = -cos(x) ⭢ wird mit x=0 zu -1
- f''''''''(x) = sin(x) ⭢ wird mit x=0 zu 0
- Wir bilden jetzt die einzelnen Glieder (Summanden) der Reihe:
- (Das Dach "^" meint hoch, das Ausrufezeichen "!" meint "Fakultät")
- 1. Glied: f(0)·x^0/(0!) = 0
- 2. Glied: f'(0)·x^1/(1!) = 1
- 3. Glied: f''(0)·x^2/(2!) = 0
- 4. Glied: f'''(0)·x^3/(3!) = -1/6
- 5. Glied: f''''(0)·x^4/(4!) = 0
- 6. Glied: f'''''(0)·x^5/(5!) = 1/120
- 7. Glied: f''''''(0)·x^6/(6!) = 0
- 8. Glied: f'''''''(0)·x^7/(7!) = -1/5040
- 9. Glied: f''''''''(0)·x^8/(8!) = 0
- Am Ende addiert man alle Werte der Glieder zusammen.
- Also: 0 + 1 + 0 - 1/6 + 0 + 1/120 + 0 - 1/5040 + 0 = 0,84 (gerundet)
- Der Sinuswert eines Winkels von 1 gibt auch im Taschenrechner gerundet 0,84.
Tipps und Hinweise
- Je näher der eingesetze x-Wert bei 0 liegt, desto ...
- schneller (weniger Glieder) erreicht man eine gute Näherung.
- Je weiter der eingesetzte x-Wert von 0 weg ist ...
- desto mehr Glieder braucht man, um einen maximal ...
- erlaubten Fehler zu unterschreiten.
- Will man schnell gute Näherung weiter weg von x haben,
- dann braucht man eine Taylor-Reihe und entwickelt sie ...
- um die Stelle x (ähnliches aber anderes Verfahren).
