Basiswissen

Als Lorentzkraft bezeichnet man die Kraft, die ein Magnetfeld auf eine elektrische Ladung ausübt. Das verblüffende ist, dass die Stärke und Richtung dieser Kraft davon abhängt, wie schnell in welche Richtung sich die Ladung durch das Magnetfeld bewegt. Das wirft die Frage auf, ob Magnetfelder unabhängig vom Beobachter existieren oder nicht.^[8]

Bildbeschreibung und Urheberrecht — Von Nordpol oben gehen die Magnetfeldlinien zum Südpol unten. Elektronen (negative Ladung) fließen vom Minuspol zum Pluspol der Leiterschaukel. Über die link-Hand-Regel kommt man zur Richtung des magnetischen Teils Lorentzkraft. © Drawn by Honina; edited by Head & Scdhönitzer (Wikimedia) ☛

Einführung zur Lorentzkraft

Traditionell und in der Schulphysik steht die Lorentzkraft nur für die Kraft, die ein Magnetfeld auf eine elektrische Ladung ausübt^[1]^[2]. Manche Autoren fassen aber auch die rein elektrostatische Coulombkraft mit unter die Lorentzkraft^[3].

MERKSATZ:

Manche Autoren zählen nur die magnetischen Kräfte zur Lorentzkraft, andere auch die rein elektrostatischen Kräfte.

Beide Ansätze sind richtig, es muss nur klar sein, ob die Lorentzkraft nur die magnetische Kraft mit den Berechnungstermen q·v·B·sinα^[4] oder q·vxB^[5] oder auch die elektrostatische Kraft mit dem Term q·E^[6] berücksichtigen soll. Beide Herangehensweisen sind richtig und werden hier zusammen kurz vorgestellt.

Die Lorentzkraft nur für B-Felder

Die zwei folgenden Formeln gelten für die Lorentzkraft im engeren Sinn. Mit ihnen kann man berechnen, welche Kraft ein B-Feld (das heißt ein Magnetfeld) auf eine elektrische Ladung q ausübt. Einen möglichen Einfluss von E-Feldern (also rein elektrostatischen Feldern, Coulomb-Feldern) berücksichtigen diese beiden Formeln nicht. Beide Formeln geben dasselbe Ergebnis. Die zweite Formel verwendet dazu das sogenannte Kreuzprodukt aus der Vektorrechnung.

F = q·v·B·sinα

F = q·v×B

Die Lorentzkraft für E- und B-Felder

Die folgenden zwei Formeln berechnen die vereinte Wirkung von B- und von E-Feldern auf eine elektrische Ladung q. Beide Formeln geben immer auch dasselbe Ergebnis. Die zweite Formel verwendet dazu das Kreuzprodukt aus der Vektorrechnung.

F = q·(E + v·B·sinα)

F = q·(E + v×B)

Legende

F = z. B. in Newton, die Lorentzkraft

q = z. B. in Coulomb, die elektrische Ladung ↗

E = z. B. in N/C, die elektrische Feldstärke ↗

v = z. B. in m/s, die Geschwindigkeit [der Ladung]

B = z. B. in Tesla, die magnetische Flussdichte ↗

α = z. B. in Grad: Winkel zwischen v und B (in Vektoren)

· = ein übliches Multiplikationszeichen ↗

× = als Kreuz das Rechenzeichen für das Kreuzprodukt ↗

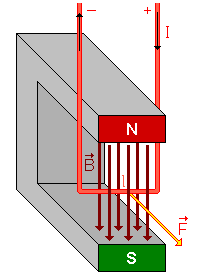
Die Linke- und die Rechte-Hand-Regel

Um die Richtung und Stärke des Anteiles des B-Feldes, also des Magnetismus, an der Lorentzkraft bestimmen zu können, muss man die Richtung kennen, in die sich eine Ladung bewegt (Daumen). Zusätzlich muss man die Richtung der Magnetfeldlinien kennen (Zeigefinger).

MERKSATZ:

Mit der Linke- oder Rechte-Hand-Regel bestimmt man die Richtung der Lorentzkraft.

Die Magnetfeldlinien gehen immer vom Nord- zum Südpol eines Magnetfeldes. Der Zeigefinger zeigt dann in Richtung der wirkenden Kraft. Für negative Ladungen (z. B. Elektronen) verwendet man die linke Hand, für positive Ladungen (z. B. Protonen oder auch Alphateilchen) verwendet man die rechte Hand:

Für positive Ladungen (Heliumkerne, Protonen) Lorentzkraft über rechte-Hand-Regel ↗

Für negative Ladungen (vor allem Elektronen) Lorentzkraft über linke-Hand-Regel ↗

Was macht die magnetische Lorentzkraft stärker?

Die Kraft ist umso stärker je schneller sich die Ladung durch das Magnetfeld bewegt,

Die Kraft ist umso stärker je senkrechter sich die Ladung zu den Magnetfeldlinien bewegt,

Die Kraft ist umso stärker je stärker das Magnetfeld ist,

Die Kraft ist umso stärker je größer die Ladung ist.

Wann wirkt die magnetische Lorentzkraft nicht?

wenn sich die Ladung parallel zu den Magnetfeldlinien bewegt,

wenn sich Ladung und Magnetfeld zueinander nicht bewegen.

wenn es keine elektrische Netto-Ladung gibt (z. B. normales Holz),

wenn es kein Magnetfeld gibt.

Übungsaufgaben zur Lorentzkraft

Einige Rechenaufgaben und Verstädnisfragen zur Lorentzkraft sind hier als Quickcheck zusammengestellt. Zu allen Fragen gibt es immer auch eine Antwort. Direkt zu den Aufgaben geht es über => qck

Die Lorentzkraft ist nicht konvervativ

Man nennt eine Kraft konservativ, wenn die von ihr verrichtete Arbeit unabhängig vom gewählten Weg zwischen zwei Punkten ist. Typische Beispiele sind die Gravitationskraft und die Coulombkraft.^[7] Die Lorentzkraft jedoch ist keine konservative Kraft ↗

Fußnoten

[1] Die Lorentzkraft als rein magnetischer Effekt: das Lehrbuch der Physik definiert die Lorentzkraft im engeren Sinn nur in Verbindung mit Magnetfeldern, nicht mit elektrischen Feldern. In: Metzler Physik" . 5. Auflage. 592 Seiten. Westermann Verlag. 2022. ISBN: 978-3-14-100100-6. Dort die Seite 237. Siehe auch Metzler (Physik) ↗

[2] Die Lorentzkraft als rein magnetischer Effekt: das Lehrbuch der Physik Dorn.Bader definiert Lorentzkraft nur über die Wirkung des Magnetfeldes: "Elektronen, die sich mit der Geschwindigkeit v snekrecht zu einem Magnetfeld mit magnetischer Flussdichte B bewegen, erfahren die Lorentzkraft mit dem Betrag F = e·v·B." Diese Definition lässt aber genauso offen, dass sich ie Elektronen auch unter anderen als 90°-Winkeln zu den Magnefeldlinien bewegen dürfen wie auch den etwaigen Einfluss eines E-Feldes. In: Dorn.Bader. Physik SII Gesamtband Gymnasium. Westermann Bildungsmedien. Braunschweig. 2023. ISBN: 978-3-14-152376-8. Dort die Seite 157.

[3] Die Lorentzkraft auch als elektrischer Effekt: "Lorentz-Kraft, die nach H. Lorentz benannte, von einem magnetischen bzw. elektromagnetischen Feld auf eine bewegte elektrische Ladung q ausgeübte Kraft FL = qE + v × B (E: elektrische Feldstärke, v: Geschwindigkeit der Ladung, B: magnetische Induktion). Der Term v × B allein wird auch magnetische Kraft Fₘ genannt." In: Spektrum Lexikon der Physik. Dort der Artikel zur "Lorentz-Kraft". Abgerufen am 6. März 2024. Online: https://www.spektrum.de/lexikon/physik/lorentz-kraft/9175

[4] q·v·B·sinα seht für das Produkt aus der Ladungsmenge q, der Geschwindigkeit v dieser Ladungsmenge relativ zum Magnetfeld, der magnetischen Flussdichte B und dem Wert des Sinus des Winkels zwischen der Richtung der Geschindigkeit v und der Magnetfeldlinien von B. zum mathematischen Hintergrund siehe auch Sinus ↗

[5] q·vxB liefert dieselben Ergebnisse wie der Term q·v·B·sinα. Doch statt mit dem Sinus zu rechnen wird dort das Kreuzprodukt des Geschwindigkeitsvektors v und des Vektors der magnetischen Flussichte B berechnet. Tatsächlich beinhaltet das Kreuzprodukt implizit auch den Sinus. Das Zeichen × ist dabei kein Buchstabe sondern ein Kreuz als Rechenzeichen für das Kreuzprodukt. Zur Mathematik davon siehe auch Kreuzprodukt ↗

[6] Die Terme q·(E + v·B·sinα) oder q·(E + v×B) stehen für die erweiterte Lorentzkraft, welche die magnetischen und elektrischen Kräfte zusammenfasst. Multipliziert man die Klammern aus, so entsteht als Term für den rein elektrischen Anteil der Lorentzkraft der Term q·E. Was dieser Term anschaulich bedeutet ist weiter erklärt im Artikel Elektrisches Feld ↗

[7] "nicht-konservative Kraft, eine Kraft, die sich nicht aus einem Potential ableiten läßt. Beispiele sind geschwindigkeitsabhängige Kräfte, wie z.B. die Reibungskraft in der Mechanik oder die Lorentz-Kraft in der Elektrodynamik." In: Spektrum Lexikon der Physik. 6 Bände. Greulich, Walter (Hrsg.) Spektrum Akademischer Verlag. Heidelberg, Berlin. 1998-2000. Dort der Artikel "Nicht-konservative Kraft". Siehe auch konservative Kraft ↗

[8] Albert Einstein zufolge existieren Magnetfelder zur relativ für einen Beobachter. Wie man das philosphisch deuten soll, ließ Einstein offen: "Ist ein punktförmiger elektrischer Einheitspol in einem elektromagnetischen Felde bewegt, so ist die auf ihn wirkende Kraft gleich der an dem Orte des Einheitspoles vorhandenen elektrischen Kraft, welche man durch Transformation des Feldes auf ein relativ zum elektrischen Einheitspol ruhendes Koordinatensystem erhält." Und: "Analoges gilt über die 'magnetomotorischen Kräfte'. Man sieht, daß in der entwickelten Theorie die elektromotorische Kraft nur die Rolle eines Hilfsbegriffes spielt, welcher seine Einführung dem Umstande verdankt,daß die elektrischen und magnetischen Kräfte keine von dem Bewegungszustande des Koordinatensystems unahbängige Existenz haben." In: Albert Einstein: Zur Elektrodynamik bewegter Körper. 1905. Siehe auch Einsteins Induktionsparadoxon ↗