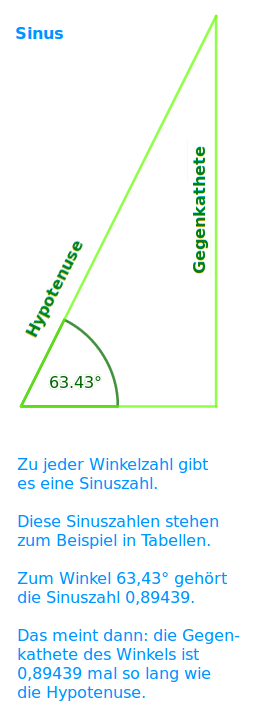
Sinus
Gegenkathete durch Hypotenuse
Basiswissen
Der Sinus ist ein Zahl die zu einem Winkel in einem rechwinkligen Dreieck gehört. Sie sagt, wie viel mal so lang die dem Winkel gegenüberliegende Kathete ist wie die Hypotenuse.
Was meint der Sinus anschaulich?
Der Sinus im engeren Sinn gehört immer zu einem festen Winkel in einem rechtwinkligen Dreieck. Zu jeder möglichen Winkelzahl (0 bis 90) gibt es einen dazugehörigen Sinuswert. Man liest ihn zum Beispiel aus einer Tabelle ab. Der Wert liegt immer zwischen 0 und 1 und sagt, wie viel mal so lang die Gegenkathete des Winkels ist, wie die Hypotenuse.
Die Formeln vorab
- Sinus = Länge der Gegenkathete durch Länge der Hypotenuse.
- Hypotenuselänge mal Sinus gleich Gegenkathetenlänge
- Gegenkathetenlänge durch Hypotenusenlänge gleich Sinus
Wo gilt der Sinus?
- Hier wird der Sinus im engeren Sinn erklärt.
- Der Sinus im engeren Sinn gilt nur für rechtwinklige Dreiecke.
- (Es gibt auch noch einen Sinus am Einheitskreis.)
Vorwissen
- Ein rechtwinkliges Dreieck hat drei Seiten.
- Die zwei Seiten direkt am rechten Winkel heißen Katheten.
- Die zwei Katheten sind die zwei kürzeren Seiten im Dreieck.
- Die Seite gegenüber vom rechten Winkel heißt Hypotenuse.
- Die Hypotenuse ist immer die längste Seite im Dreieck.
- In einem rechtwinkligen Dreieck gibt es immer genau eine Hypotenuse.
Was meint Sinus?
- Der Sinus gehört immer zu einem Winkel.
- Es ist immer ein Winkel in einem rechtwinkligen Dreieck.
- Aber: der Winkel darf nie der rechte Winkel selbst sein.
- Man sucht sich einen der beiden anderen Winkel aus.
- Man sagt: "Sinus von alpha" oder kurz "Sinus alpha".
- Der Sinus von alpha sagt sagt, dann, wieviel mal ...
- so lang die Gegenkathete ist wie die Hypotenuse.
Zahlenbeispiel
- Wenn man sagt, der Sinus von alpha sei 0,5, dann heißt das:
- Die Gegenkathete von alpha ist 0,5 mal so lang wie die Hypotenuse.
- Wenn man sagt, der Sinus von alpha sei 0,1, dann heißt das:
- Die Gegenkathete von alpha hat die 0,1fache Länge der Hypotenuse.
Sinuswert aus Tabelle
- Wenn man den Winkel alpha kennt, dann kann man in einer ...
- Tabelle nachsehen, welcher Sinuswert dazu gehört.
- Siehe dazu => Sinustabelle Grad
Eigenschaften
- Gegenkathete geteilt durch Hypotenuse gibt den Sinus von alpha.
- Der Sinus ist das Verhältnis von Gegenkathete zu Hypotenuse.
- Hypotenuse mal Sinus gibt die Länge der Gegenkathete.
- Der Sinus ist immer eine Zahl zwischen 0 und 1.
- Jeder Winkelwert hat einen eigenen Sinuswert.
- Die Sinuswerte für alle Winkel stehen in Tabellen.
Abkürzungen
- GK meint => Gegenkathete
- AK meint => Ankathete
- HY meint => Hypotenuse
Berechnungen
=> Hypotenuse über Sinus
=> Gegenkathete über Sinus
=> Winkel über Sinus
Sonstiges
- Im Lexikon "sinus 40" zeigt den entsprechenden Sinuswert an.
- Die Mehrzahl laut Duden ist "Sinusse" oder einfach "Sinus".
- Sinus ist Latein und heißt so viel wie "Bucht".
