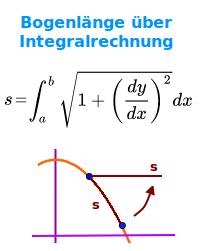
Bogenlänge über Integralrechnung
∫√ [1+(f'(x))²]·dx
© 2016
- 2025
Definition|
Formel|
Legende|
Zahlenbeispiel|
Überprüfung der Berechnung|
Schwierigkeitsgrad der Berechnung
Definition
Auf einem Funktionsgraphen (Kurve) sind zwei Punkte gegeben. Die Bogenlänge s zwischen diesen Punkten ist definiert als der Abstand des gerade gestreckt gedachten Bogens. Die Länge kann mit Hilfe eines Integrals berechnet werden.
Formel
- s = ∫√ [1+(f'(x))²]·dx
Legende
- f(x) = die gegebene 👉 Funktionsgleichung
- a = x-Wert des linken Punktes auf dem Funktionsgraphen 👉 linke Integrationsgrenze
- b = x-Wert des rechten Punktes auf dem Funktionsgraphen 👉 rechte Integrationsgrenze
- s = von x=a bis x=b die 👉 Bogenlänge
- ∫ = das 👉 Integralzeichen
- f'(x) 👉 erste Ableitung
Zahlenbeispiel
- f(x) = -x²+6
- a=1 und b=2
- Formel: s = ∫√ [1+(f'(x))²]·dx
- Einsetzen: s = ∫√ [1+(-2x)²]·dx
- Vereinfachen: s = ∫√ [1+4x²]·dx
- Aufleiten, Grenzen einsetzen und berechnen:
- s ≈ 3,168
Überprüfung der Berechnung
Man kann die Plausibilität über einen maßstabsgerecht gezeichneten Funktionsgraphen überprüfen: man legt dann auf der Kurve des Graphen einen Faden zwischen die beiden Punkte, streckt den Faden und misst über ein Lineal nach.
Schwierigkeitsgrad der Berechnung
- Für konkrete Probleme müssen die Aufleitungen von Wurzelfunktionen bestimmt werden.
- Die entsprechenden Terme sind meist nicht mit einfachen Aufleitungsregeln zu bestimmen.
- Man schlägt entsprechend nach in Tabellen zu 👉 Aufleitungen