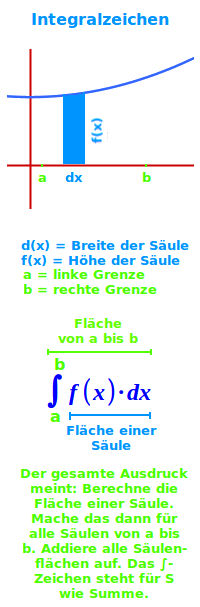
Integralzeichen
∫f(x)·dx anschaulich
© 2016
- 2025
Basiswissen
∫f(x)·dx liest man als: Das Integral von f(x) in den Grenzen von a bis b. Eine Zahl für a steht dabei immer links unten am Integralzeichen und b oben links am Integralzeichen. Es meint: bilde eine Stammfunktion zu f(x). Diese Stammfunktion nennt man dann F(x). Rechne dann F(b)-F(a). Das Ergebnis nennt man das Integral. Das ist hier ausführlich und anschaulich erklärt.
Eine Säule
- Man hat einen Funktionsgraphen in einem xy-Koordinatensystem.
- Irgendwo auf der Achse wählt man eine Stelle x aus, z. B. x=2.
- Über diesem Punkt x auf der x-Achse zeichnet man dann eine schmale Säule:
- Ihre Breite nennt man dx. Ihre Höhe geht bis zum Graphen von f(x):
- Also gibt der Funktionswert f(x) auch die Säulenhöhe an.
- Multipliziert man die Höhe f(x) mit der Breite dx ...
- erhält man den Flächeninhalt dieser Säule:
- Säulenfläche = f(x)·dx
Viele Säulen
- Man kann nun zwei Stellen auf der x-Achse auswählen:
- Die linke Stelle nennt man a, die rechte Stelle b.
- Man kann gedanklich von a bis b einzelne Säulen bilden.
- Jede Säulenfläche für sich berechnet man über f(x)·dx.
- Wenn die Säulen keine Lücken haben und sich nicht überlappen, ...
- dann kann man alle diese Säulenflächen zwischen a und b aufaddieren.
- Sie entsprechen dann einigermaßen gut der Flächen zwischen f(x) und der x-Achse.
- Der Ausdruck: ∫f(x)·dx meint genau das: addiere Säulenflächen auf.
- Das Zeichen ∫ ist ein stilisiertes S und steht für eine Summe.
- Mehr dazu auch unter 👉 Säulenmethode
Grenzwert
- Nun kann man gedanklich die Säulen zwischen a und b immer schmaler machen.
- Will man die gesamte Fläche von a nach b unter dem Graphen ausfüllen, enstehen dadurch immer mehr Säulen.
- Im Extremfall lässt man die Säulenbreite gegen 0 laufen und erhält dadurch Richtung unendlich viele Säulen.
- Dabei wird der Fehler in der Berechnung der Fläche unter dem Graphen von f(x) immer kleiner.
- Dass man diesen Grenzwert bildet wird über das Integralzeichen ∫ mit angedeutet.
dx oder ∆x
- Man unterscheide ∆x und dx.
- Man schreibt ∆x für reale breiten von fest gedachten Säulen.
- Man schreibt dx für die Säulenbreite im Grenzwertdenken.
- Das dx ist ein sogenanntes 👉 Differential
a und b
- Die Zahlen a und b nennt man die Integrationsgrenzen.
- Das a steht immer links, das b steht immer rechts.
- a heißt auch 👉 linke Integrationsgrenze
- b heißt auch 👉 rechte Integrationsgrenze
Fußnoten
- [1] Lothar Papula: Mathematik für Ingenieure und Naturwissenschaftler. Ein Lehr- und Arbeitsbuch für das Grundstudium. Band 1. 14. Auflage, 2019. ISBN: 978-3-658-05619-3. Verlag Springer Vieweg. Seite 433 ff.
- [2] Ein Lexikon des Jahres 1859 definiert das Wort Integralzeichen: "Jede Function nun, deren Differential f (x) dx ist, heißt, in sofern sie aus ihrem Differential erst gefunden werden soll, das Integral von f (x) dx u. wird bezeichnet durch ∫ f (x) dx, für sie ist demnach d ∫ f (x) dx = f (x) dx. Das vorgesetzte Zeichen ∫ heißt das Integralzeichen. Aus einem Integral die ursprüngliche Function herleiten heißt integriren, die Herleitung Integration" Der Artikel nennt dann einige Anwendungen der Integralrechnung und geht abschließend kurz auf die Geschichte der Integralrechnung ein. In: Pierer's Universal-Lexikon, Band 8. Altenburg 1859, S. 941. Online: http://www.zeno.org/nid/20010180923