A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 9 Ω
Das Banner der Rhetos-Website: zwei griechische Denker betrachten ein physikalisches Universum um sie herum.

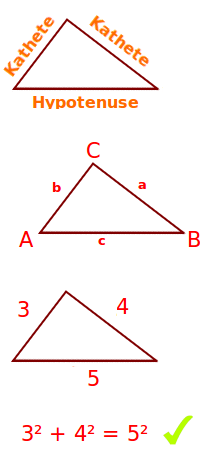
Satz des Pythagoras

a² + b² = c²

© 2016 - 2025


Basiswissen｜ Einführung zum Satz des Pythagoras｜ Formel für den Satz des Pythagoras｜ Legende｜ Was sind die Katheten (a und b) und was die Hypotenuse (c)?｜ Der Satz des Pythagoras rein rechnerisch｜ Der Satz des Pythagoras geometrisch gedeutet｜ Der praktische Nutzen｜ Die längste Seite berechnen (Hypotenuse)｜ Eine der zwei kürzeren Seiten berechnen (Kathete)｜ Gilt der Satz des Pythagoras immer?｜ Kann man den Satz beweisen?｜ Exkurs I: der Satz des Pythagoras als Wahrsagerei｜ Exkurs II: der Satz des Pythagoras und gekrümmte Räume｜ Aufgaben zum Satz des Pythagoras｜ Fußnoten


Basiswissen


a² + b² = c² ist der Satz des Pythagoras kurz als Formel[3] geschrieben: man hat ein rechtwinkliges Dreieck mit drei Seiten: a, b und c. Das kleine c steht dabei für die längste Seite, die Hypotenuse. Man misst die Länge jeder der drei Seiten. Dann multipliziert man die Länge jeder Seite mit sich selbst, quadriert sie also. Man erhält drei Zwischenergebnisse: a², b² und c². Dann addiert man a² und b². Die daraus entstehende Summe ist immer gleich (oder sehr nahe bei) c². Kurz: a²+b² = c²



Bildbeschreibung und Urheberrecht
Man sieht drei rechtwinklige Dreiecke übereinander.☛


Einführung zum Satz des Pythagoras


Der Satz des Pythagoras gilt nur für rechtwinklige Dreiecke (genau ein 90°-Winkel) und alle rechtwinkligen Dreiecke. Er besagt: multipliziert man die Längen der beiden kürzeren Seiten (Katheten) mit sich selbst und addiert diese Zwischenergebnisse zusammen, erhält man immer dasselbe Ergebnis wie bei der Multiplikation der längsten Seite (Hypotenuse) mit sich selbst. Mit Hilfe dieser Formel genügt es, bei einem rechtwinkligen Dreieck die Länge von zwei Seiten zu kennen. Man kann dann die Länge der dritten Seite immer berechnen.

Formel für den Satz des Pythagoras


  • a² + b² = c²

Legende



Was sind die Katheten (a und b) und was die Hypotenuse (c)?


  • a² meint dasselbe wie a mal a.
  • Der Satz des Pythagoras gilt für alle rechtwinkligen Dreiecke.
  • Die Hypotenuse liegt immer gegenüber vom rechten Winkel ↗
  • Die Hypotenuse ist immer die längste Seite im Dreieck.
  • Das c in der Formel steht immer für die Länge der Hypotenuse.
  • Die Katheten sind die Schenkel des rechten Winkels.
  • Die Katheten sind immer die zwei kürzeren Seiten.
  • Das a ist die Länge von einer der beiden Katheten.
  • Das b ist die Länge der anderen der beiden Katheten.

Der Satz des Pythagoras rein rechnerisch


  • Man nimmt die Länge einer Kathete mit sich selbst mal.
  • Mit sich selbst malnehmen nennt auch hoch zwei rechnen oder quadrieren ↗
  • Man nimmt die Länge der anderen Kathete mit sich selbst mal.
  • Man addiert diese beiden Ergebnisse.
  • Wenn man die Länge der Hypotenuse mit sich selbst malnimmt, …
  • kommt dabei immer dieselbe Zahl heraus.

Der Satz des Pythagoras geometrisch gedeutet


  • Man nimmt eine der zwei Katheten.
  • Man nennt diese Seite und ihre Länge a.
  • Man betrachtet sie als eine von vier Seiten von einem Quadrat ↗
  • Man zeichnet dann damit ein Quadrat, das ist das Quadrat „über der ersten Kathete“.
  • Man macht dasselbe dann mit der zweiten Kathete und mit der Hypotenuse.
  • Die zweite Kathete und ihre Länge nennt man b, die Hypotenuse nennt man c.
  • Man hat dann also insgesamt drei Quadrate gezeichnet.
  • a mal a oder kurz a² gibt den Inhalt des ersten Quadrates.
  • b mal b oder kurz b² gibt den Inhalt des zweiten Quadrates.
  • c mal c oder kurz c² gibt den Inhalt des dritten Quadrates.
  • Dann addiert man die ersten beiden Flächen.
  • Diese Summe gibt genau die Fläche des dritten Quadrates.
  • Man sagt: die Summe der Quadrate über den zwei Katheten, …
  • ist vom Zahlenwert her gleich dem Quadrat über der Hypotenuse.

Der praktische Nutzen


Der Satz des Pythagoras war spätesten seit 1500 v. Chr. den Babylonieren[4], seit vielleicht 500 v Chr. den Indern und seit spätestens 100 v. Chr den Chinesen bekannt. Der große praktische Nutzen besteht darin, dass man nur zwei Seiten eines rechtwinkligen Dreiecks kennen muss. Die dritte fehlende Seite kann man dann berechnen. Das eröffnet die Möglichkeit, die Länge von Diagonalen, etwa als Stütztbalken in einem Raum oder auch die Breite von Seen zu berechnen, ohne dass man dabei die gesuchten Strecken selbst abschreiten muss.

Die längste Seite berechnen (Hypotenuse)


  • Bekannt sind: a und b
  • Z. B. a=5 und b=12
  • Man geht aus von: a²+b² = c²
  • c ist die Länge der gesuchten Hypotenuse.
  • Man formt die Gleichung um nach c:
  • a²+b² = c² | auf beiden Seiten die Wurzel ziehen
  • Wurzel von (a²+b²) = c
  • Einsetzen: Wurzel von (5²+12²) = 13
  • Die gesuchte Länge von c ist: 13

Eine der zwei kürzeren Seiten berechnen (Kathete)


  • Man geht aus von: a²+b² = c²
  • c ist die Hyptonuse, also die längste Seite.
  • a ist eine der zwei Katheten, b die andere.
  • Es ist für a und b egal, wer die längere ist.
  • Man formt um nach zum Beispiel a:
  • a² + b² = c² | -b²
  • a² = c²-b² | Wurzel ziehen
  • a = Wurzel aus (c²-b²)
  • Zahlenbeispiel: c=5 und b=4. Wie lang ist a?
  • Einsetzen: a = Wurzel aus (5²-4²)
  • a = Wurzel aus (25-16) = 3
  • Die gesuchte Kathete hat die Länge 3.

Gilt der Satz des Pythagoras immer?


Solange man rechtwinklige Dreiecke auf flachen, ungekrümmten Flächen zeichnet, etwa auf einem glatten Stück Papier auf einem Tisch, dann stimmt der Satz immer. Interessant ist jetzt ein Gedankenexperiment, bei dem der Satz zunehmend nicht mehr stimmt. Man stellt sich die Erde als völlig perfekte Kugel vor. Wir leben dann gedanklich auf dieser Kugeloberfläche. Nun zeichnen wir ein kleines rechtwinkliges Dreieck. Wenn wir die Seitenlängen messen und damit den Satz des Pythagoras überprüfen wird er (abgesehen von kleinen Messungenauigkeiten) immer sehr gut aufgehen, also stimmen. Machen wir das Dreieck aber gedanklich sehr groß, dann geht die Gleichung immer schlechter auf. Der Grund ist dass war nicht auf einer glatten ebenen Fläche zeichnen, sondern auf einer gekrümmten Kugeloberfläche[1]. Tatsächlich gibt es ein großes Gebiet der Geometrie, das sich mit Figuren auf Kugeloberflächen beschäftigt. Das ist die sogenannte sphärische Geometrie. Ein sehr interessanter Fall zu diesem Gedanken ist das von uns so genannte Galapagos-Dreieck ↗

Kann man den Satz beweisen?


Ja, im Jahr 2024 gelang es Schülern aus den USA sogar, insgesamt 5 neue Beweise vorzulegen. Die Beweise wurden in einem wissenschaftlichen Artikel auf Englisch veröffentlich.[2]

Exkurs I: der Satz des Pythagoras als Wahrsagerei


Der Satz des Pythagoras ist recht einfach zu verstehen und anzuwenden. An ihm zeigt sich aber gleichzeitig auch eine sehr tiefgründige und begehrte Eigenschaft vieler (natur)wissenschaftlicher oder mathematischer Erkenntnisse: man kann damit etwas aus der Zukunft voraussagen. Das ist zunächst nicht offensichtlich. Man kann den Satz aber etwas umformulieren, und dann wird es deutlich:

MERKSATZ:

wenn man die Längen von zwei kurzen Seiten in einem rechtwinkligen Dreieck misst, kann man nach einer einfachen Rechnung mit großer Genauigkeit vorhersagen, was das Messergebnis sein wird, wenn man die Länge der längsten Seite misst.

Damit kann man zumindest für einen Aspekt in die Zukunft blicken. Man sieht nicht die ganze Zukunft, aber einen Teil davon kann man genau voraussagen. Das heißt umgekehrt aber auch, dass die Zukunft, also die Entwicklung der Welt, sich wahrscheinlich an den Satz des Pythagoras "halten wird", sie wird ihn nicht verletzten. Damit wird die Zukunft für Menschen zumindest etwas voraussehbarer, planbarer, weniger chaotisch. Die Idee, dass die Welt bewusst so eingerichtet ist, dass wir als Menschen in ihr gewisse Regeln erkennen können, um unsere eigene Zukunft auch gestalteten zu können, bezeichnet man in der Philosophie auch als Intelligibilität ↗

Exkurs II: der Satz des Pythagoras und gekrümmte Räume


Der Satz des Pythagoras gilt für alle rechtwinkligen Dreiecke auf einer ebenen, perfekt flachen Fläche, etwa einem perfekt flachen Tisch. Er gilt aber nicht für sehr große rechtwinklige Dreiecke: die Stadt Mogadischu liegt an der Ostküste Afrikas, nahe am Äquator. Man stelle sich jetzt einen Piloten vor, der in einer geraden Linie von Mogadischu aus zum Nordpol fliegt und dabei exakt die geflogene Strecke misst. Ein anderer Pilot fliegt von Mogadischu aus parallel zum Äquator nach Osten, bis zum Stadtstaat Singapur in Südostasien. Auch dieser Pilot habe die Strecke gemessen. Die zwei Flugstrecken treffen in Mogadischu in einem Winkel von genau 90° aufeinander. Nun fliege ein dritter Pilot in direkter gerader Linie vom Nordpol nach Singapur. Auch dieser Pilot soll wieder die Strecke messen. Diese Strecke ist dann die Hypotenuse eines rechtwinkligen Dreiecks. Hier sind die drei gemessenen Entfernungen:

  • 1. Kathete: Mogadischu-Nordpol: 9781 km
  • 2. Kathete: Mogadischu-Singapur: 6503 km
  • Hypotenuse: Nordpol-Singapur: 9864 km

Wendet man den Satz des Pythgaroras an, kommt man auf folgende Gleichung: 9781²+6503²=9864². Ausgerechnet gibt das die (ziemlich falsche) Aussage: 137956970 = 97298496. In Worten müssten dann etwa 137 Millionen gleich 97 Millionen sein. Die Abweichung ist viel zu groß, als dass sie durch kleine Messfehler oder ein nur geringfügige Abweichung von der Rechtwinkligkeit des Dreiecks herrührt. Tatsächlic ist der Grund für die große Abweichung, dass das Dreieck nicht in einer flachen Ebene sondern auf einer Kugel gedacht werden muss. Und für Dreiecke auf Kugelflächen gilt der Pythagoras in der einfachen Form a²+b²=c² nicht mehr. Man hat jetzt eine gekrümmte Fläche und benötigt die sogenannte sphärische Geometrie.

Auf einer gekrümmten Fläche, etwa der Erdoberfläche, gilt "der Pythagoras" also nicht mehr. Der folgende Gedanke führt jetzt zur Idee eines gekrümmten Raumes. Angenommen, man würde im Weltraum mit Hilfe von Laserlichtern ein riesiges Dreieck aufspannen. Drei Raumschiffe bilden die Ecken. Die Raumschiffe könnten sich so lange zueinander bewegen, bis ein perfekt rechtwinkliges Dreieck entsteht. Und wenn Licht sich geradlinig ausbreitet[8], dann sind die Strecken zwischen den Ecken des Dreiecks gerade Linien. Wenn aber auch hier der Satz des Pythagoras trotz sorgfältigster Messung nicht passen sollte, welchen Schluss soll man das ziehen? Stimmt etwas mit dem Raum an sich nicht? Genau diese Frage führt zur Idee, dass auch der Raum vielleicht nicht "flach" sondern "gekrümmt" ist, in Analogie zu einer gekrümmten Fläche. Siehe dazu den Artikel gekrümmter Raum ↗


Aufgaben zum Satz des Pythagoras


  • => qck [gemischte Aufgaben]

Fußnoten


  • [1] Bei Gesetzen spricht man von einem sogenannten Gültigkeitsbereich. Das ist der Bereich der Wirklichkeit für den ein Gesetz ausreichend gut passt. In der Mathematik entspricht dieser Gedanke dem Definitionsbereich.
  • [2] Bis zum Jahr 2024 gab es lediglich zwei anerkannte Beweise des Satzes des Pythgaros. Schüler in den USA fügten dem im Jahr 2024 insgesamt 5 neue und eigenständige Beweise hinzu. Die Ergebnisse wurden in einer Fachzeitschrift auf Englisch veröffentlicht. Jackson, N., & Johnson, C.: Five or Ten New Proofs of the Pythagorean Theorem. The American Mathematical Monthly, 131(9), 739–752. (2024). Online: https://doi.org/10.1080/00029890.2024.2370240
  • [3] 1906, der Satz des Pythagoras als Beispiel für eine Formel: "Formel (lat. formula), für besondere Fälle entweder ausdrücklich vorgeschriebene oder durch den Gebrauch eingeführte Worte, Redensarten oder Wendungen, z. B. Gebets-, Rechtsformeln. In der Mathematik versteht man unter F. die Darstellung von Größen und Sätzen durch die Zeichensprache der Mathematik, z. B. ist (a + b) die F. für die Summe der beiden Größen a und b; a² + b² = c³ die F. für den pythagoreischen Lehrsatz etc. Über Chemische Formeln s.d." In: Meyers Großes Konversations-Lexikon, Band 6. Leipzig 1906, S. 768. Online: http://www.zeno.org/nid/20006624812
  • [4] Im antiken Babylon war der Satz seit etwa 1500 vor Christus bekannt: In: Helmuth Gericke: Mathematik in Antike und Orient. Berlin 1984, S. 33 f.
  • [5] Die Inder listeten um 600 vor Christus schon verschiedene pythagoräische Tripel auf und nutzen den Satz in seiner allgemeinen Bedeutung. In: Helmuth Gericke: Mathematik in Antike und Orient. Berlin u. a. 1984, S. 66–69.
  • [6] Jean-Claude Martzloff: A History of Chinese Mathematics. Berlin u. a. 1997, S. 124, 126.
  • [7] Zum Beispiel Landvermesser, Markscheider und Geographen benötigen die sphärische Geometrie. Sie ist mathematisch deutlich schwieriger als die Geometrie flacher Ebenen. Siehe mehr unter sphärische Geometrie ↗
  • [8] Dass Licht sich geradlinig ausbreitet, stimmt nicht ganz: es wird etwas durch Masse abgelenkt. Das ist eine Folgerung aus Einsteins allgemeiner Relativitätstheorie ↗