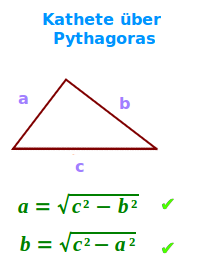
Kathete über Pythagoras
Berechnen
© 2016
- 2025
Basiswissen|
Was muss gegeben sein?|
Was ist die allgemeine Lösungsidee?|
Zahlenbeispiel|
Wie berechnet man die Hypotenuse?
Basiswissen
b=√(c²-a²): man hat ein rechtwinkliges Dreieck und kennt die Länge c der längsten Seite (die Hypotenuse ) sowie die Länge a einer der beiden Katheten. Damit kann man immer die Länge der anderen Kathete ausrechnen. Das ist hier mit einem Zahlenbeispiel erklärt.
Was muss gegeben sein?
- Es muss um ein rechtwinkliges Dreieck gehen.
- Bei anderen Dreiecken funktioniert diese Methode nicht.
- Von dem Dreieck muss die Länge c der Hypotenuse gegeben sein.
- Von dem Dreieck muss die Länge a oder b einer Kathete gegeben sein.
- Wir nennen hier die gegebene Kathetenlänge a.
- Siehe auch:
Was ist die allgemeine Lösungsidee?
- Man rechnet die Hypotenusenlänge c zum Quadrat, das gibt c².
- Man rechnet die Kathetenlänge a zum Quadrat, das gibt a².
- Man rechnet dann Differenz aus, also c²-a².
- Aus dem Ergebnis zieht man dann die Wurzel.
- Das ist die gesuchte Länge b der anderen Kathete.
- Hintergrund ist der 👉 Satz des Pythagoras
Zahlenbeispiel
- Die Länge c der gegebenen Hypotenuse: 17 cm
- Die Länge a der anderen Kathete: 15 cm
- c² gibt 289.
- a² gibt 225.
- c²-a² gibt 64.
- Daraus die Wurzel gibt 8.
- Die andere Kathete ist 8 cm lang.
Wie berechnet man die Hypotenuse?
Hat man die Länge der beiden Katheten gegeben, kann man immer die noch unbekannte Länge der Hypotenuse berechnen über c² = a²+b². Das ist erklärt unter 👉 Hypotenuse über Pythagoras