Mathematik
In dem Term 9x³ - 8x² + 11x + 7 sind die 9, die -8, die 11 und auch die 7 Koeffizienten. Das wird hier kurz mit Beispielen erklärt. => Ganzen Artikel lesen …
… mit wenig Aufwand viel erreichen => Effizienz
Liste verschiedener
Beiwerte oder Koeffizienten werden häufig in der Technik verwandt. Hier stehen Beispiele wie der Pearson-Koeffizient (Statistik), der Koeffizient einer Matrix oder der Wärmeleitkoeffizient. => Ganzen Artikel lesen …
Effizienz
Wenig Aufwand, viel Nutzen
Man kann die Gleichung 0=x²-30x+200 mit wenig und mit viel Aufwand lösen. Mit viel Aufwand ist es effektiv, mit wenig effizient. Als Effizienz bezeichnet man das Verhältnis von Nutzen zu Aufwand. [1] Dazu stehen hier einige Beispiele aus verschiedene Fachgebieten. => Ganzen Artikel lesen …
Leitkoeffizient
Faktor vor höchster Potenz
Der Leitkoeffizient ist der Faktor vor der höchsten Potenz von x. Beispiel: 4x³+8x²-5. Die höchste Potenz von x ist hier das x³. Der dazugehörige Faktor ist die 4. Also ist die 4 der Leitkoeffizient des ganzen Ausdrucks. => Ganzen Artikel lesen …
… wie 5x³ ableiten, siehe unter => Ableiten über Faktorregel
Physik
Der Absorptionskoeffizient, auch Dämpfungskonstante oder linearer Schwächungskoeffizient, ist ein Maß für die Verringerung der Intensität elektromagnetischer Strahlung beim Durchgang durch ein gegebenes Material. Er wird in der Optik und in Bezug auf Röntgenstrahlung und Gammastrahlung verwendet. Sein übliches Formelsymbol ist in der Optik α (kleines alpha) und speziell bei Röntgen- und Gammastrahlung μ (kleines my). Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… oft mit alpha abgekürzt, siehe unter => Ausdehnungskoeffizienten
… kleine alpha in der Physik => thermischer Längenausdehnungskoeffizient
Arten
Thermischer Ausdehnungskoeffizient, Wärmeausdehnungskoeffizient oder Holzausdehnungskoeffizient. Hier stehen einige Beispiele und Wertelisten. => Ganzen Artikel lesen …
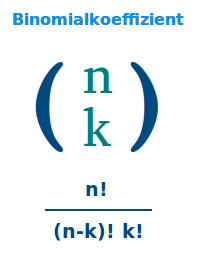Binomialkoeffizient
Formel
n über k = n! durch [k! mal (n-k)!]. Mit Zahlen: 5 über 3 gäbe 5! durch 3!·(5-3)!. Ausgerechnet gibt das genau 10. Die Berechnung wird hier ausführlich erklärt. => Ganzen Artikel lesen …
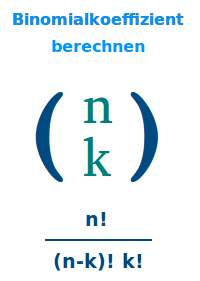
Binomialkoeffizient berechnen
Wie man n über k ausrechnet (Binomialkoeffizient)
n über k = n! / [(n-k)!k!] => Ganzen Artikel lesen …
… ist per Definition immer 1, mehr unter => Binomialkoeffizient
… ist per Definition immer 1, mehr unter => Binomialkoeffizient
… ist per Definition immer 1, mehr unter => Binomialkoeffizient
Zahlenliste
10 über 4 gibt 210: hier steht eine auftsteigend sortierte Liste mit häufigen Werten für n über k => Ganzen Artikel lesen …
… aus der Statistik, siehe unter => Korrelationskoeffizient nach Pearson
… aus der Statistik, siehe unter => Korrelationskoeffizient nach Pearson
… aus der Statistik, siehe unter => Korrelationskoeffizient nach Pearson
… auch cp-Wert genannt, siehe unter => Druckbeiwert
… siehe unter => Elastizitätsmodul
… siehe unter => Elastizitätsmodul [mit Werteliste]
Werteliste
Von extrem wenig Gleitreibung bei geschmierten Stahl (0,01) bis zu einer sehr starken Gleitreibung von zum Beispiel einem Fahrrad-Gummi-Reifen auf Asphalt (0,5): hier steht eine Liste mit Zahlenwerten aus der Technik. => Ganzen Artikel lesen …
Zahlenliste
Vom Schlittschuh mit 0,03 bis zum Reifen auf Beton mit 0,8: hier steht eine Liste mit typischen Werten der sogenannten Haftreibunskoeffizienten. Das Typische Formelzeichen ist das µ (kleines griechisches my) mit einem rechts tiefgestellten großen H. [1] Die Haftreibung ist ein zusätzlicher Widerstand, bevor ein Körper auf einer Unterlage in Bewegung gesetzt werden kann. [1] => Ganzen Artikel lesen …
Definition
Der Begriff ist unüblich, wäre aber sinnvoll: er könnte die Ausdehnung von Holz bei Erwärmung meinen. Er könnte aber auch die Ausdehnung bei Feuchtigkeitsaufnahme meinen. In der Praxis spielt das Letztere eine größere Rolle, also die Ausdehnung bei Feuchtigkeit. Siehe dazu => Holzquellung
wegen Feuchtigkeit, man unterscheidet das
- => Schwindmaß
Wärmelehre
Es gibt Gase, die sich beim Zusammendrücken erwärmen, zum Beispiel Luft beim Aufpumpen eines Fahrrades. Andere Gase werden aber auch kälter, wenn man sie zusammendrückt. Welcher Effekt - und wie stark - in der Wirklichkeit eintritt, das sagt der sogenannte Joule-Thomson-Koeffizient. Die übliche Abkürzung ist ein kleines griechisches my μ. Die weitere Theorie dazu geht über den Rahmen dieses online-Lexikons hinaus. Mit dem angegebenen Stichwort kann man aber an anderer Stelle weiter recherchieren. => Ganzen Artikel lesen …
… ist per Definition immer 1, mehr unter => Binomialkoeffizient
Jede Zahl in einer Matrix
Eine Matrix ist eine tabellarische Anordnung von Zahlen in Zeilen (quer) und Spalten (hoch). Jede Zahl in einer Matrix heißt Koeffizient. Man spricht auch von einer => Koeffizientenmatrix
Zahlenwerte
Matrizen sind tabellenartigen Strukturen von Zahlen. Die reinen Zahlen an sich heißen Koeffizienten. Mehr zur Defininition unter => Koeffizient einer Matrix
… jede Zahl in einer Matrix, mehr unter => Koeffizient einer Matrix
Definition | Zahlenbeispiel
Die Terme 4x+8y-25 und -25+4x+8x sind koeffizientengleich. Das ist hier mit Beispielen kurz erklärt. => Ganzen Artikel lesen …
LGS
Eine auf reine Zahlen reduzierte Darstellung eines Linearen Gleichungssystems in tabellarischer Form nennt man eine Koeffizientenmaxtrix. Das ist hier mit einem Beispiel erklärt. => Ganzen Artikel lesen …
… für kubische oder höhere Funktionen => Satz über rationale Nullstellen
… eine Zahl für ein => Zusammenhangsmaß
