ℜ
Physik Chemie Grundschule Mathematik I Mathematik II Wissen
Kurze Worte Worte nach Alter Terme Rechner
Mathfeed Physfeed Philfeed
Das Lexikon Die Mission Die Autoren Copyright Impressum
Physik Nachhhilfe 5-10 Physik Nachhilfe 11-13 Chemie Nachhilfe 5-13 Mathe Nachhilfe 5-8 Mathe Nachhilfe 9-10 Mathe Nachhilfe 10-13
☰
1: Gerade

Übersicht

Eine Gerade in der Mathematik ist eine Linie ohne Ecken, Lücken, Kurven oder Enden: sie ist unendlich lang gedacht. Die kürzeste Verbindung zwischen zwei Punkten liegt immer auf einer Geraden. Hier werden Geraden in verschiedenen Teilgebieten der Mathematik kurz vorgestellt. => Ganzen Artikel lesen …
2: Geraden

In der Mathematik: Klassifizierung und Arten

In der Mathematik werden Geraden sowohl innerhalb der Geometrie (2D und 3D) als auch in der Funktionen- und Gleichungslehre behandelt. In der Anylsis spielen sie als Veranschaulichung von linearen Funktionen (Geradengleichung) eine grundlegende Rolle. Es folgen jetzt verschiedene Typen von Geraden. => Ganzen Artikel lesen …
3: Dekade

10 Tage

Als Dekade bezeichnet man heute einen Zeitraum von 10 Tagen. Die Bezeichnung geht zurück auf die frühe Zeit nach der französischen Revolution, als man eine Woche mit 10 Tagen einführen wollte. Das hat sich aber nie durchgesetzt. Im Englischen hingegen steht decade für ein => Jahrzehnt
4: Erde

♁ Als Planet

Das Wort Erde ohne Artikel geschrieben ist ein lockerer Stoff aus natürlichem Bodenmaterial. Die Erde -also mit Artikel geschrieben - steht für den Planeten Erde. Hier stehen einige Fakten zur Erde als Planet. => Ganzen Artikel lesen …
5: Ungerade

Mathematik

1; 3; 5; 7; 9 und 11: alle natürlichen oder ganzen Zahlen, die nicht in der Zweierreihe stehen nennt man ungerade. Neben den ungeraden Zahlen gibt es aber noch andere Dinge in der Mathematik, die man als ungerade bezeichnet. Diese sind hier kurz vorgestellt. => Ganzen Artikel lesen …
6: Gerät

… technischer Apparat, siehe zum Beispiel => Elektrogeräte
7: 2D-Gerade

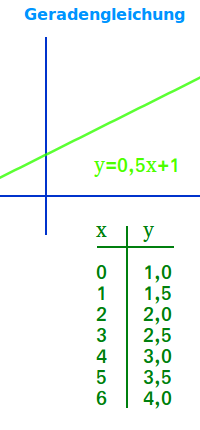
xy-Koordinatensystem

y = 4x+2 - das ist die Gleichung einer typischen Gerade in einem xy-Koordinatensystem, also in einem zweidimensionalen oder kurz 2D-Koordinatensystem. Dazu hier mehr zur Definition. => Ganzen Artikel lesen …
8: 2D-Schnittpunkte von Geraden bestimmen

… Anleitung unter => Schnittpunkte von zwei Geraden graphisch bestimmen
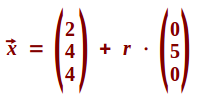9: 3D-Gerade

Gerade in ein einem 3D-Koordinatensystem

Eine Gerade in sich ist ein eindimensionales Gebilde: man kann sich auf ihr nur hin und her bewegen, in einer Dimension. Betrachtet man die Gerade aber als platziert in einem dreidimensionalen Koordinatensystem, kann man sie als 3D-Gerade bezeichnen. => Ganzen Artikel lesen …
10: 3D-Geradenform Gleichung

… mit Stütz- und Richtungsvektor, siehe unter => Parameterform der Geraden
11: 3D-Geradengleichung

… mit Stütz- und Richtungsvektor, siehe unter => Parameterform der Geraden
12: Abstand Gerade-Gerade

… siehe unter => Abstand von Gerade zu Gerade
13: Abstand Gerade

… eine Übersicht zu verschiedenen Fällen steht unter => Geradenabstände
14: Abstand Gerade zu Gerade

… siehe unter => Abstand von Gerade zu Gerade
15: Abstand Geraden

… eine Übersicht zu verschiedenen Themen steht unter => Geradenäbstande
16: Abstand von Gerade zu Ebene

Formel

Verläuft die Gerade nicht parallel zur Ebene, dann haben Gerade und Ebene immer einen Schnittpunkt. In diesem Fall ist der Abstand also immer 0 Längeneinheiten. Verlaufen Gerade und Ebene aber parallel zueinander, dann kann der Abstand berechnet werden. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
17: Abstand von Gerade zu Gerade

Lösungsweg

Zwei zueinander parallele und nicht identische Geraden haben überall denselben Abstand zueinander. Sind die zwei Geraden nicht parallel zueinander dann nennt man sie windschief. Für zwei windschiefe Geraden gibt es immer genau einen kürzesten Abstand. Hier steht eine stark verkürzte Anleitung für die Berechnung dieses Abstandes. => Ganzen Artikel lesen …
18: Abstand von Gerade zu Punkt

… in, der Vektorrechnung, siehe unter => Abstand von Punkt zu Gerade
19: Abstand von Punkt zu Gerade

Lösungsformel

Abstand heißt hier: die kürzeste Entfernung. Kurz vorgestellt wird eine Berechnungsmethode mit Hilfe von Vektoren und Geraden (analytische Geometrie). => Ganzen Artikel lesen …
20: Abstand zweier Geraden

… siehe unter => Abstand von Gerade zu Gerade
21: Abstand zwischen Geraden

… siehe unter => Abstand von Gerade zu Gerade
22: Abstand zwischen zwei Geraden

… siehe unter => Abstand von Gerade zu Gerade
23: Abstandsaufgabe mit Geraden

… verschiedene Fälle stehen unter => Geradenabstände
24: Abstandsformel Gerade

… verschiedene Fälle stehen unter => Geradenabstände [Übersicht]
25: Abstandsprobleme mit Geraden

… verschiedene Fälle stehe unter => Geradenabstände
26: Achsenabschnittsform der Geradengleichung

Lineare Funktion

x:a+y:b=1 ist die sogenannte Abschsenabschnittsform einer Geraden, das heißt des Graphen einer linearen Funktion. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
27: Achsenabschnittsform einer Geraden

Lineare Funktion

x/a+y/b=1 ist die sogenannte Abschsenabschnittsform einer Geraden [1] mit dem a als x-Achsenabschnitt und dem b als y-Achsenabschnitt. Die Gerade ist hier gedeutet als eine lineare Funktion. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
28: Allgemeine Form der Geradengleichung

Analysis

C = Ax + By nennt man auch die allgemeine Form einer Geradengleichung oder einer linearen Funktion. Das y entspricht dabei auch dem Funktionsterm f(x). Stellt man nach y um, erhält man y = -(A/B)·x + C/B. Diese Form ist eher ungebräuchlich im Sinne einer Funktionsgleichung. Sie ist aber eine typische Form für eine => lineare Gleichung mit zwei Unbekannten
29: Analytische Geometrie Gerade

… in der Vektorrechnung, siehe unter => 3D-Gerade
30: Antiparallele Geraden

… für verschiedene Objekte, siehe unter => nicht parallel
31: Anzahl Geradenschnittpunkte

Wieviele Schnittpunkte Geraden haben können

=> Ganzen Artikel lesen …
32: Anzahl Schnittpunkte von zwei Geraden

Wie viele Schnittpunkte zwei Geraden haben können

Zwei Geraden in einem x-y-Koordinatensystem können keine, genau einen oder unendlich viele Schnittpunkte haben. => Ganzen Artikel lesen …
33: Aus Text Geradengleichung aufstellen

… Kurztipps und Aufgaben, siehe unter => Geradengleichung aus Text
34: Aus Texten Geradengleichung aufstellen

… Kurztipps und Aufgaben, siehe unter => Geradengleichung aus Text
35: Aus Texten Geradengleichungen aufstellen

… Kurztipps und Aufgaben, siehe unter => Geradengleichung aus Text
Zur Startseite von Rhetos
Startseite
Impressum
© 2010-2023


Startseite Impressum Feedback © 2010-2023