Abweichung
Definition
Angenommen eine Raumtemperatur soll stets 20 °C beträgten. Das ist der Soll-Wert. Die Tatsächliche Temperatur sei aber gerade nur 18 °C. Das ist dann der Ist-Wert. Die Differenz beträgt 2 °C. Das ist die Abweichung. Das ist hier kurz erläutert. => Ganzen Artikel lesen …
Beispiel
Beispiel: Gebäudeversicherung sollte eigentlich Hochwasserschäden mit abdecken, also im Schadensfall die Schäden bezahlen. Doch aufgrund der zunehmenden Extremwetterereignisse, schließen zunehmend viele Versicherungen solche Schäden ausdrücklich aus. Siehe auch => Haftpflichtversicherung
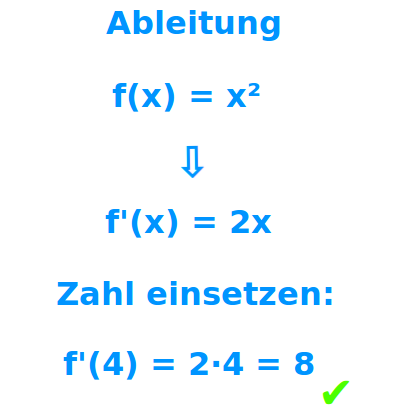
Ableitung
f'(x)
Die Ableitung steht einmal für die Steigung (als Zahl) an einem bestimmten Punkt auf einem Funktionsgraphen. Präziser spricht man hier auch vom Ableitungswert. Als Ableitung bezeichnet man auch eine Funktion f'(x), die für jeden x-Wert die dort geltende Steigung am Graphen angibt.[1][2] Präziser wäre hier: Ableitungsfunktion => Ganzen Artikel lesen …
Böschung
Knick in an sich sanftem Gefälle
Man betrachtet eine flach abfallende (oder ansteigende) Geländefläche. Hat diese Fläche in einem Bereich eine deutlich größere Steigung als darunter oder darüber, dann ist dieser Bereich erhöhter Steigung eine Böschung. Ist die Böschung auf natürliche Weie entstanden, spricht man von einem Hang. => Ganzen Artikel lesen …
Messabweichung
Definition
Angenommen ein kleiner Holzstab ist genau 20 cm lang. Ein Lineal zeigt aber 20,3 cm an. Dann ist die Messabweichung hier genau 0,3 Zentimeter. Die Berechnung ist immer: gemessener Wert minus den wahren oder den richtigen Wert. Das Ergebnis kann damit auch negativ sein. Das ist hier näher erklärt. => Ganzen Artikel lesen …
… Ein Messgerät genau machen: gesetztlich gefordert, amtlich bestätigt, mehr unter => Messgerät einstellen
Brechung
Physik
Trifft ein Strahl [2], eine Welle [4] oder ein Teilchenstrom (z. B. Photonen) an eine Grenze zwischen zwei durchsichtigen Medien (z. B. Luft in Glas oder Luft in Wasser) oder ändert sich die Geschwindigkeit der Welle in einem Medium, dann kann es zu einer Änderung der Richtung kommen. Diesen Effekt nennt man in der Physik Brechung oder auch Refraktion [3]. Siehe mehr zu diesem Effekt unter => Brechung (Physik)
… empfohlener Begriff für => absoluter Fehler
… siehe unter => Standardabweichung aus Binomialverteilung
… in der Statistik dasselbe wie die => mittlere absolute Abweichung
Statistik
Die empirische Standardabweichung, auch Stichprobenstreuung genannt [1], ist die Standardabweichung, die tatsächlich durch Beobachtung oder Messung von Daten entstanden ist. Das Gegenteil wäre eine rein theoretische Bestimmung einer Standardabweichung, das wäre nicht empirisch, sondern theoretisch. Die empirische Standardabweichung s² ist eines von mehreren sogenannten Streuungsmaßen. Hier ist kurz vorgestellt, wie man die empirische Standardabweichung berechnet. => Ganzen Artikel lesen …
Statistik
Durchschnittliche Entfernung zum gemeinsamen Durchschnitt: die mittlere absoute Abweichung ist eines von mehreren Streuungsmaßen. Bei der mittleren linearen Abweichung einer Zahlenmenge berechnet man für jede Zahl ihren Abstand zum gemeinsamen Durchschnitt: Durchschnitt minus Zahl. Dabei können auch negative Werte werden entstehen. Will man das vermeiden, nimmt die mittlere absolute Abweichung. BDas heißt, bei Minuszahlen lässt man das Minus einfach weg. Man sagt auch, dass man von allen Abweichungen den Betrag bildet. Das ist hier mit einem Beispiel kurz erkläutert. => Ganzen Artikel lesen …
Zahlenbeispiel
Die mittlere absolute Abweichung der Zahlen 1, 4 und 7 ist 2: die mittlere absolute Abweichung ist der durchschnittliche Abstand der Zahlen einer Liste zu ihrem gemeinsamen Durchnitt. Das ist hier ausführlich erklärt. => Ganzen Artikel lesen …
Statistik
Besser: „Mittlere absolute Abweichung“: die „mittlere lineare Abweichung“ in der Statistik ist ein irreführender Begriff. Berechnet man sie, erhält man für alle Listen von Zahlen immer das Ergebnis 0. Hier steht, warum man besser von einer betragsmäßigen oder mittleren absoluten Abweichung spricht. => Ganzen Artikel lesen …
Statistik
Das Ergebnis wird für alle Zahlenlisten immer die Zahl 0 ergeben. Die Berechnung ist aber aus theoretischer Sicht interessant. Sie führt zu einem weiteren Gedanken, der hier ausgeführt ist. => Ganzen Artikel lesen …
… s², Sigma² oder var(x), ein Streuungsmaß, heißt auch => Varianz
Bei der mittleren quadratischen Abweichung wird für jeden Datenwert das Quadrat (hoch zwei) des Abstandes zum arithmetischen Mittel berechnet, daher der Name. Der gebräuchliche Fachbegriff für dieses Streuungsmaß ist => Varianz
Definition
Das folgende Programm in der Programmiersprache PHP berechnet die Standardabweichung von den Zahlen in einer Feldvariablen (array). Innerhalb des Programm steht auch eine kurze Beschreibung der Mathematik zur Standardabweichung. Am Ende stehen einige Testdatensätze. => Ganzen Artikel lesen …
… ist in der Statistik die => Varianz
… in der Statistik heißt die mittlere quadratische Abweichung => Varianz
… empfohlener Begriff für => relativer Fehler
… Erklärung mit Zahlenbeispiel unter => Standardabweichung aus Varianz
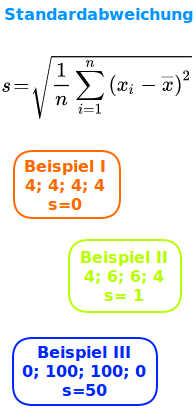
Standardabweichung
σ: Ein Streuungsmaß aus der Statistik
Die Standardabweichung Sigma gibt an, wie weit die Zahlen einer Zahlenliste von ihrem gemeinsamen Mittelwert entfernt sind. Die Zahlenliste 3;3;3;3 hat eine Standardabweichung von 0. Die Zahlenliste 1;1;5;5 hat eine Standardabweichung von 2. Hier wird kurz erklärt, was die Standardabweichung als Streuungsmaß bedeut und wie man sie berechnet. => Ganzen Artikel lesen …
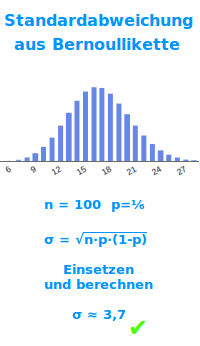
Standardabweichung aus Bernoulli-Kette
σ = √(n·p·(1-p))
Einer Binomialverteilung liegt immer einer Bernoulli-Kette als Modell zugrunde. Die Formel oben gilt deshalb sowohl für Bernoulli-Ketten als auch Binomialverteilungen. Eine ausführliche Erklärung steht unter => Standardabweichung aus Binomialverteilung
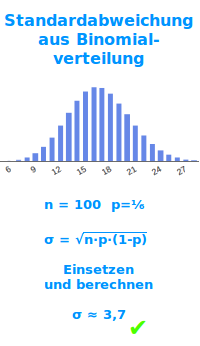Standardabweichung aus Binomialverteilung
σ = √(n·p·(1-p))
Die Standardabweichung gibt in etwa an, wie weit die Trefferhäufigkeiten im Schnitt von ihrem gemeinsamen Durchschnittswert entfernt sind. Sie spielt auch eine Rolle im Zusammenhang mit dem Satz von Moivre-Laplace. Beides ist hier kurz vorgestellt. => Ganzen Artikel lesen …
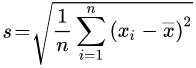Standardabweichung aus Datenliste
Berechnung
Zum Beispiel für die Liste der Zahlen 4, 7 und 10: wie man das das kleine Sigma oder s berechnet, wenn man eine Datenliste, das heißt eine Liste aus Zahlen, gegeben hat: das ist hier kurz mit einem Zahlenbeispiel erklärt. => Ganzen Artikel lesen …
… Erklärung mit Zahlenbeispiel unter => Standardabweichung aus Varianz
… Erklärung mit Zahlenbeispiel unter => Standardabweichung aus Varianz
Berechnung
Die Varianz und daraus die Wurzel gibt die Standardabweichung. Wenn die Varianz 4,0 ist, dann ist die Standardabweichung 2,0. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… Erklärung mit Zahlenbeispiel unter => Standardabweichung aus Varianz
… Erklärung mit Zahlenbeispiel unter => Standardabweichung aus Varianz
… Erklärung mit Zahlenbeispiel unter => Standardabweichung aus Datenliste
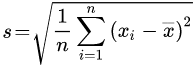Standardabweichung berechnen
Übersicht
Die Standardabweichung Sigma kann für Datenreihen (Zahlenlisten) aber auch aus anderen gegebenen Werten berechnet berechnet werden. Hier werden kurz verschiedene Formeln dazu vorgestellt. => Ganzen Artikel lesen …
… Erklärung mit Zahlenbeispiel unter => Standardabweichung aus Varianz
… Erklärung mit Zahlenbeispiel unter => Standardabweichung aus Varianz
… mehrere Möglichkeiten unter => Standardabweichung berechnen
