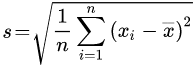Standardabweichung berechnen
Übersicht
Basiswissen
Die Standardabweichung Sigma kann für Datenreihen (Zahlenlisten) aber auch aus anderen gegebenen Werten berechnet berechnet werden. Hier werden kurz verschiedene Formeln dazu vorgestellt.
Vorab
- Die Standardabweichung wird oft mit einem kleinem Sigma oder s abgekürzt.
- Eine Erklärung beziehungsweise Definition steht unter Standardabweichung ↗
- Hier folgen jetzt verschiedene Berechnungsmethoden:
Aus der Varianz
- Angenommen die Varianz s² ist also Zahlenwert schon gegeben.
- Dann einfach daraus die Wurzel ziehen. Das ist alles.
- Mehr unter Standardabweichung aus Varianz ↗
Aus einer Datenliste
- Die Summe der quadrierten Abstände aller Zahlen ...
- zu ihrem gemeinsamen arithmetischen Mittel berechnen.
- Diese Summe durch die Anzahl n teilen und daraus die Wurzel ziehen.
- Ausführliches Zahlenbeispiel unter Standardabweichung aus Datenliste ↗
Aus einer Binomialverteilung
- In Worten: die Wurzel aus [n mal p mal (1-p)]
- n = Länge der Bernoulli-Kette
- p = Erfolgswahrscheinlichkeit eines Gliedes der Kette
- Mehr unter Standardabweichung aus Binomialverteilung ↗
Aus einer Bernoulli-Kette
- Die Wurzel aus [n mal p mal (1-p)]
- n = Länge der Bernoulli-Kette
- p = Erfolgswahrscheinlichkeit eines Gliedes der Kette
- Mehr unter Standardabweichung aus Bernoulli-Kette ↗
Aufgaben dazu
Einige Aufgaben zur Berechnung der Standardabweichung sind hier als Quickcheck zusammengestellt. Zu allen Aufgaben gibt es auch eine Lösung. Direkt zu den Aufgaben geht es über => qck
