Basiswissen

Feste Sigma-Umgebungen

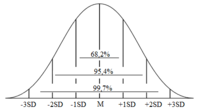
• 68,27 % der Daten liegen in der Ein-Sigma-Umgebung ↗
  

• 95,45 % der Daten liegen in der Zwei-Sigma-Umgebung ↗
  

• 99,73 % der Daten liegen in der Drei-Sigma-Umgebung ↗
  

Markante Prozentangaben

• 99 % aller Werte haben eine Abweichung von höchstens 2,576 Sigma vom Median.
  

• 95 % aller Werte haben eine Abweichung von höchstens 1,960 Sigma vom Median,
  

• 90 % aller Werte haben eine Abweichung von höchstens 1,645 Sigma vom Median,
  

• 50 % aller Werte haben eine Abweichung von höchstens 0,675 Sigma vom Median,
  

• 10 % aller Werte liegen um mehr als das 1,28fache Sigma über dem Median.
  

• 5 % aller Werte liegen um mehr als das 1,64fache Sigma über dem Median.
  

• 1 % aller Werte liegt um mehr als das 2,33fache Sigma über dem Median.
  

Wofür gelten diese Regeln?

• Für alle normalverteilten Daten gelten die sogenannten Sigmaregeln.
  

• Diese Regeln näherungsweise auch für lange Bernoulli-Ketten.
  

• Bernoulli-Kette ergeben die sogenannte Binomialverteilung.
  

• Siehe auch Binomialverteilung ↗
  

• Siehe auch Normalverteilung ↗
  

Wie bestimmt man Sigma?

• Aus einer Binomialverteilung: σ = √(n·p·(1-p) Standardabweichung aus Binomialverteilung ↗
  

• Aus einer Datenliste Standardabweichung aus Datenliste ↗
  

• Aus der Varianz Standardabweichung aus Varianz ↗