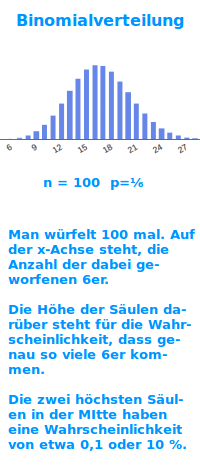
Binomialverteilung
B(n,k,p)
Basiswissen
Als Binomialverteilung bezeichnet man eine übersichtsartige Darstellung der Wahrscheinlichkeiten aller möglichen Ergebnisse einer Bernoulli-Kette: Die Verteilung gibt an, wie sich die 100 % dass irgendetwas passiert auf die einzelnen Ergebnisse verteilen, daher das Wort Verteilung. Eine Binomialverteilung kann eine Tabelle, ein Graph oder ein Histogramm sein. Das ist hier näher erklärt.
Was ist eine Bernoulli-Kette?
Jeder Binomialverteilung aus der Stochastik liegt eine sogenannte Bernoulli-Kette zugrunde. Eine Bernoulli-Kette ist eine Aneineiandereihung sogenannter Bernoulli-Experimente. Ein Bernoulli-Experiment ist ein Experiment bei dem man immer nur zwei Ausgänge unterscheidet. Den einen Ausgang nennt man Treffer den anderen zum Beispiel nicht-Treffer. Bei einer Bernoulli-Kette führt man solche Bernoulli-Experimente zum Beispiel 4 mal aus, man sagt: die Bernoulli-Kette hat die Länge n=4. Für die ganze Bernoulli-Kette kann man dann fragen, wie groß die Wahrscheinlichkeit ist, dass man genau 0 oder 1 oder 2 oder 3 oder sonsteine Anzahl von Treffern hat. Man sagt allgemein: wie groß ist die Wahrscheinlichkeit P bei einer Bernoulli-Kette genau k Treffer zu haben.
Was ist die Binomialverteilung?
Das ist die Darstellung der einzelnen Wahrscheinlichkeiten für alle möglichen Werte von k für eine konkrete Bernoulli-Kette. Anders gesagt: die Vertreilung gibt an, wie sich die Gesamtwahrscheinlichkeit 1 oder 100 % auf die einzelnen möglichen Ausgänge verteilt.
Was wäre ein Beispiel?
Man würfelt 5 mal. Es kann sein, dass dabei 0, 1, 2, 3, 4 oder 5 mal eine Sechs kommt. Jede dieser Anzahlen k von Sechsern hat eine Wahrscheinlichkeit "zu kommen". Die Darstellung der Wahrscheinlichkeiten für alle möglichen Trefferzahlen k nennt man die Binomialverteilung:
- k = 0, also 0 Sechser: P(X=0) ist etwa 0,16
- k = 1, also 1 Sechser: P(X=1) ist etwa 0,32
- k = 2, also 2 Sechser: P(X=2) ist etwa 0,29
- k = 3, also 3 Sechser: P(X=3) ist etwa 0,16
- k = 4, also 4 Sechser: P(X=4) ist etwa 0,05
- k = 5, also 5 Sechser: P(X=5) ist etwa 0,01
Was bedeutet das?
Einer Binomialverteilung liegt eine sogenannte Bernoulli-Kette zugrunde: Man führt n Versuche durch. Bei jedem Versuch unterscheidet man nur: Treffer oder nicht-Treffer. Das kleine k ist dann die Anzahl von Treffern, wenn man n Versuche macht. Die Verteilung sagt, wie sich die 100 % Wahrscheinlichkeit dass irgendeines der möglichen k-Werte kommt auf die einzelnen k-Wert verteilt.
Wofür steht die Höhe der Säulen?
Es gibt zwei Möglichkeiten, die aber unmittelbar direkt zusammenhängen. Eine Säule steht immer für eine bestimmte Anzahl k von Treffern, die man bei n Teilversuchen erhält. Die Höhe der dazugehörigen Säule kann a) die Wahrscheinlichkeit angeben, dass diese Trefferhäufigkeit k bei n Versuchen kommt. Oder b) die Säulenhöhe steht für die tatsächliche Anzahl von k Treffern bei n Teilversuchen. Die Wahrscheinlichkeit einer Säule multipliziert mit der Länge der Bernoulli-Kette n ergibt dabei immer die Häufigkeit der Trefferzahl k. Die Unterscheidung ist beispielsweise wichtig für die Interpretation der Standardabweichung. Diese bezieht sich immer auf die Interpretation b. Mehr dazu unter Standardabweichung aus Binomialverteilung ↗
Was sind Standard-Formeln?
- B(n,k,p) oder P(X=k):
- P(X=k) = [n über k] · [p hoch k] · [(1-p) hoch (n-k)]
- Standardabweichung sigma = Wurzel [n·p·(1-p)]
- Varianz sigma² = n·p·(1-p)
- Erwartungswert mü = n·p
Legende
- P(X=k) meint: die Wahrscheinlichkeit, dass die Trefferzahl X genau k ist
- n = Länge der Kette, Anzahl der Wiederholungen
- k = Anzahl der Treffer
- p = Wahrscheinlichkeit für Treffer bei einem Versuch
- n über k ist der Binomialkoeffizient ↗
Beispiele
- Man würfelt mit 4 normalen Spielwürfeln gleichzeitig.
- Wie groß ist die Wahrscheinlichkeit, dann genau 3 Sechser zu würfeln?
- Eine Sechs zu würfeln wäre dann ein Treffer.
- Gesucht ist also P(X=3).
- Mit der Formel gibt das genau 5/243 oder etwa 2 %.
- Wenn man also 100 mal mit 4 Würfeln würfelt, dann ...
- hat man meistens etwa 2 mal genau 3 Sechser gewürfelt.
Was ist eine diskrete Verteilung?
- Eine Binomialverteilung ist eine diskrete Verteilung.
- Man unterscheidet diskrete von stetigen Wahrscheinlichkeitsverteilungen.
- In vielen Erklärungen wird darauf hingewiesen, dass die Binomialverteilung diskret ist.
- Diskret heißt: in eindeutigen gegeneinander abgetrennten Schritten ohne fließende Übergängen.
- Diskret sind hier die einzelnen Ergebnisse, also die k-Werte.
- Man kann 0, 1, 2, 3, 4 und so weiter Treffer haben.
- Es macht keinen Sinn von 1,23 oder 0,4444 Treffer zu sprechen.
- Mehr dazu unter diskret ↗
