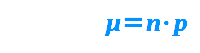Erwartungswert aus Binomialverteilung
my = n·p
© 2016
- 2025
Basiswissen
Was ist die durchschnittliche Anzahl k von Treffern in einer Bernoulli-Kette der Länge n? Die Antwort ist n·p. Das ist der Erwartungswert.
Formel
- μ = n·p
Legende
- μ = kleines griechisches My, der 👉 Erwartungswert
- n = Länge der 👉 Bernoulli-Kette
- p = Erfolgswahrscheinlichkeit bei einem 👉 Bernoulliversuch
Beispiel
- Man würfelt 30 mal mit einem normalen Spielwürfel.
- Man zählt immer die Anzahl k der 6en, die man dabei erhält.
- Man wiederholt diesen Versuch sehr oft, theoretisch unendlich oft.
- Wie viele 6er würde man dann im Schnitt (arithmetisches Mittel) erhalten?
- Rechnung: my = n·p, also: my = 30·(1/6) = 5
- Man würde im Schnitt 5 Sechsen würfeln, wenn man 30 Würfel wirft.
- Die Zahl 5 ist hier der Erwartungswert.