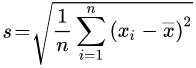Standardabweichung aus Datenliste
Berechnung
© 2016
- 2025
Basiswissen
Zum Beispiel für die Liste der Zahlen 4, 7 und 10: wie man das das kleine Sigma oder s berechnet, wenn man eine Datenliste, das heißt eine Liste aus Zahlen, gegeben hat: das ist hier kurz mit einem Zahlenbeispiel erklärt.
Datenliste
- Gegeben sein muss eine Datenliste, z. B. Längen von Nüssen in cm:
- Hier ist eine Beispielliste mit drei Werten: 4 cm | 7 cm | 10 cm
- Man lässt von dieser Datenliste die Einheiten weg, falls vorhanden:
- Man hat dann nur eine Zahlenliste: 4 | 7 | 10
Berechnung
- Zuerst berechnet man von der Zahlenliste das 👉 arithmetisches Mittel
- Arithmetisches Mittel x-Strich meint dasselbe wie Durchschnitt.
- Für die Datenliste oben wäre das die 7.
- Dann von jeder Zahl (oft xi) den Abstand zum Mittelwert berechnen
- Das wären im Beispiel: 3 | 0 | 3
- Dann von allen Abständen das Quadrat bilden
- Das wären im Beispiel: 9 | 0 | 9
- Die Summe der Quadrate durch die Anzahl n der Werte teilen
- Das gäbe im Beispiel die Zahl 6.
- Daraus die Wurzel ziehen, gäbe etwa 2,45
- Das ist die Standardabweichung Sigma oder klein s.
- Siehe auch 👉 Standardabweichung
Fußnote
- [1] Ein Lehrbuch der Mathematik definiert: "Die Wurzel aus der mittleren quadratischen Abweichung […] der Werte der Häufigkeitsverteilung vom arithmetischen Mittel [x-quer] wird als empirische Standardabweichung [s-quer] bezeichnet." In: Elemente der Mathematik. Nordrhein-Westfalen. Qualifikationsphase. Leistungskurs. Schroedel Westermann. Druck vom Jahr 2021. ISBN: 978-3-507-8799-1-1. Dort die Seite 327. Siehe auch 👉 empirische Standardabweichung