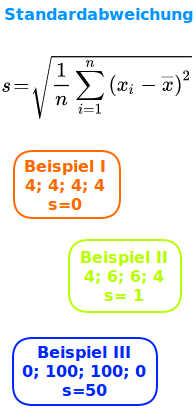
Standardabweichung
σ: Ein Streuungsmaß aus der Statistik
© 2016
- 2025
Basiswissen|
Was ist ein Streuungsmaß?|
Was bedeutet die Standardabweichung allgemein?|
Was bedeutet eine kleine Standardabweichung?|
Was bedeutet eine große Standardabweichung?|
Schreibweisen für die Standardabweichung|
Wozu ist dieses Streuungsmaß gut?|
Wie berechnet man die Standardabweichung?|
Synonyme|
Fußnoten
Basiswissen
Die Standardabweichung Sigma gibt an, wie weit die Zahlen einer Zahlenliste von ihrem gemeinsamen Mittelwert entfernt sind. Die Zahlenliste 3;3;3;3 hat eine Standardabweichung von 0. Die Zahlenliste 1;1;5;5 hat eine Standardabweichung von 2. Hier wird kurz erklärt, was die Standardabweichung als Streuungsmaß bedeut und wie man sie berechnet.
Was ist ein Streuungsmaß?
- Das sind Zahlen zur Beschreibung von Zahlenlisten.
- Ein Streuungsmaß sagt in etwa, wie weit auseinander Zahlen einer Liste liegen.
- Je weiter sie streuen, desto weiter liegen sie voneinander entfernt.
- Die Standardabweichung σ ist dementsprechend ein 👉 Streuungsmaß
Was bedeutet die Standardabweichung allgemein?
- Sie gehört immer zu einer Zahlenliste.
- Sie selbst ist immer eine positive Zahl.
- Sie sagt in etwa, wie weit die Zahlen im Schnitt ...
- von ihrem gemeinsamen Durchschnitt entfernt liegen.
- Durchschnitt ist dasselbe wie 👉 arithmetisches Mittel
- Dabei werden aber sogenannte Ausreißer etwas stärker bewertet.
Was bedeutet eine kleine Standardabweichung?
Die Zahlenliste 1;1;3;3; hat die Standardabweichung 1. Die Zahlenliste 1;1;1;1 hat als Standardabweichung sogar 0: eine kleine Standardabweichung sagt, dass die Zahlen einer Liste alle sehr nahe bei ihrem gemeinsamen arithmetischen Mittel (Durchschnitt) liegen.
Was bedeutet eine große Standardabweichung?
Die Zahlenliste 1;20;80;99 hat die Standardabweichung von ungefähr 47. Das ist recht viel. Die Zahlen 50,50,50,144 hat als Standardabweichung genau 47. Eine hohe Standardabweichung kann heißen, dass a) die Zahlen einer Liste alle recht weit von ihrem gemeinsamen Durchschnitt entfernt sind, oder b) dass die meisten Zahlen zwar nah am gemeinsamen Durchschnitt liegen, es aber einen weit davon entfernten Ausreißer gibt. Der Ausreißer im zweiten Beispiel war die Zahl 144. Die Standardabweichung überbetont die Wirkung von einem statistischen 👉 Ausreißer
Schreibweisen für die Standardabweichung
- Die Abkürzung dafür ist oft ein kleiner Buchstabe 👉 s
- Üblich ist auch ein σ 👉 kleines griechisches Sigma
Wozu ist dieses Streuungsmaß gut?
Zahlenlisten vergleicht man oft über den Durchschnitt. So könnte man sagen, dass das durchschnittliche Jahreseinkommen pro Person in zwei verschiedenen Ländern 50 Tausend Euro betrage. Man könnte jetzt meinen, dass die Menschen in diesen Ländern vom Geld her ähnlich gut dastehen. Es könnte aber sein, dass in dem einen Land einige ganze wenige Leute sehr, sehr viel Geld verdienen und die große Mehrheit so gut wie gar nichts. In dem anderen Land hingegen verdienen wirklich fast alle ähnlich viel. Solche Unterschiede können Streuungsmaße erfassen. Je größer die Werte auseinander liegen, desto größer ist auch der Zahlenwert der Standardabweichung.
Wie berechnet man die Standardabweichung?
Dazu gibt es verschiedene Methoden, je nachdem was gegeben ist. Bei längeren Zahlenlisten wird die Berechnung schnell sehr aufwändig, man benutzt dann meisten Taschenrechner oder Computerprogramme. Lies mehr unter 👉 Standardabweichung berechnen
Synonyme
Fußnoten
- [1] Die empirische Standardabweichung: "Die Wurzel aus der mittleren quadratischen Abweichung […] der Werte der Häufigkeitsverteilung vom arithmetischen Mittel [x-quer] wird als empirische Standardabweichung [s-quer] bezeichnet." In: Elemente der Mathematik. Nordrhein-Westfalen. Qualifikationsphase. Leistungskurs. Schroedel Westermann. Druck vom Jahr 2021. ISBN: 978-3-507-8799-1-1. Dort die Seite 327. Siehe auch 👉 empirische Standardabweichung