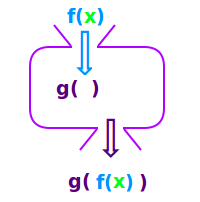
Verkettete Funktion
g∘f = g(f(x))
© 2016
- 2025
Basiswissen|
Die Grundidee einer Verkettung|
Wie schreibt und spricht man die Verkettung?|
Zwei Funktionen verketten: Schritt-für-Schritt|
Was sind die innere und die äußere Funktion?|
Eine Funktionsverkettung sicher erkennen|
Was ist eine Verknüpfung?|
Wie leitet man verkettete Funktionen ab?|
Wie leitet man verkettete Funktionen auf?|
Fußnoten
Basiswissen
Der Funktionswert y einer Funktion wird als Argument x in eine andere Funktion eingesetzt. Diese Hintereinanderausführung zweier (oder auch mehrerer) Funktionen nennt man eine Verkettung von Funktion oder auch eine Komposition, man spricht auch von einer zusammengesetzten Funktion[2]. Das ist hier näher erklärt.
Die Grundidee einer Verkettung
Man hat zwei Funktionen. Wenn man den Funktionswert der ersten Funktion ausrechnet und dann als x-Wert für die zweite Funktion benutzt, dann hat man die beiden Funktionen verkettet. Wenn man zum Beispiel erst f(x)=2+x ausrechnet für x=3, dann erhält man den Funktionswert 5. Diese 5 setzt man dann als x-Wert, auch Argument genannt, in die zweite Funktion g(x)=x² ein. Dann erhält man als Ergebnis 25. Dieses Hintereinander-Ausführen von zwei oder mehr Funktionen ist die Verkettung.
Wie schreibt und spricht man die Verkettung?
- g∘f spricht man als "g nach f" oder "g komponiert mit f" oder "g Kringel f".
- Alternativ schreibt man g(f(x)) und spricht: g von f von x
- Siehe auch unter g∘f ↗
Zwei Funktionen verketten: Schritt-für-Schritt
- Gegeben seien g(x) = x² und f(x) = 2+x
- Gebildet werden soll die Verkettung: g∘f
- Man spricht g verkettet mit f und schreibt: g(f(x))
- Die Reihenfolge von g und f ist dabei wichtig.
- Man betrachtet den Funktionsterm von g(x).
- Der Funktionsterm ist der Term rechts vom Gleichzeichen.
- Jedes x im Funktionsterm von g(x) ersetzt man durch eine leere Klammer.
- Im Beispiel schreibt man dann für die Verkettung: g(f(x)) = ( )²
- In diese leeren Klammern schreibt man dann den Funktionsterm von f(x).
- Im Beispiel: g(f(x)) = (2+x)² ✓
Was sind die innere und die äußere Funktion?
Bei verketteten Funktion spricht man oft von einer inneren und einer äußeren Funktion. Im Beispiel g(f(x)) = (x+2)² wäre f(x) = x+2 die innere Funktion und g(x) = x² ist dann die äußere Funktion. Es gibt eine einfache Methode, um die innere und äußere Funktion zu unterscheiden. Man versucht gedanklich, den Funktionswert für die Verkettung mit x=1 auszurechnen. Den Funktionsterm, den man zuerst ausrechnen muss, gehört dann immer zur inneren Funktion. Bei g(f(x)) = (x+2)² muss man zuerst x+2 ausrechnen. Also ist x+2 der Term der inneren Funktion. Dann rechnet man mit dem Ergebnis weiter hoch zwei. Das Quadrieren ist dann die äußere Funktion.
- g(f(x)) = (x+5)³ -> x+5 ist die innere Funktion, ()³ ist die äußere Funktion
- g(f(x)) = e^(2x) -> 2x ist die innere Funktion, e^() ist die äußere Funktion
- g(f(x)) = sin(x²) -> x² ist die innere Funktion, sin() ist die äußere Funktion
Eine Funktionsverkettung sicher erkennen
- Wir betrachten das Beipiel: g(f(x)) = (2+x)²
- Diese Verkettung entstand aus g(x) = x² und f(x) = 2+x
- Man betrachtet nun nur die die rechte Seite der Funktionsgleichung ↗
- Die rechte Seite einer Funktionsgleichung heißt auch Funktionsterm ↗
- Kommt eine unabhängige Variable vor (meist das x), dann gilt:
- Das x darf nur innerhalb der inneren Funktion vorkommen.
- Außerhalb der inneren Funktion darf x nicht vorkommen.
- Das Ergebnis der inneren Funktion gilt als Ausgangszahl für die äußere Funktion.
- Siehe auch Verkettete Funktionen ↗
Was ist eine Verknüpfung?
- Eine Verknüpfung ein Überbegriff, Verkettung davon ein Sonderfall.
- Bei einer Verknüpfung werden zwei oder mehr Funktionen irgendwie verbunden:
- Beispiel: f(x)=x und g(x)=e^x werden verknüpft zu f(x)·g(x)=x·e^x
- Als Verknüpfung möglich sind zum Beispiel die Addition, Multiplikation oder jede beliebige andere Operation.
- Bei einer Verkettung hingegen muss der Wert der einen Funktion immer als Argument in die andere eingesetzt werden.
- Mehr dazu unter Verknüpfung ↗
Wie leitet man verkettete Funktionen ab?
Der übliche Merksatz dazu ist: innere Funktion abgeleitet mal äußere Funktion abgeleitet. Sind f(x)=x² und g(x)=cos(x) verkettet zu v(x)=cos(x²) dann ist die Ableitung v'(x)=-2x·sin(x²). Das ist ausführlich erklärt im Artikel Ableiten über Kettenregel ↗
Wie leitet man verkettete Funktionen auf?
- Man soll die Aufleitung finden für: g(f(x))·f'(x)
- Lies mehr dazu unter Integrieren über Substitution ↗
Fußnoten
- [1] Lothar Papula: Mathematik für Ingenieure und Naturwissenschaftler. Ein Lehr- und Arbeitsbuch für das Grundstudium. Band 1. 14. Auflage, 2019. ISBN: 978-3-658-05619-3. Verlag Springer Vieweg. Hier das Kapital "Kettenregel", Seite 337.